Mit Tagesdauer ist die Zeit innerhalb von 24 h gemeint, in der die Sonne über dem Horizont steht. Dabei sei hier vereinfachend angenommen, daß die sich Sonne als punktförmige Lichtquelle in einem Abstand von der Erde befindet, der sehr viel größer als der Erdradius ist. Die Erdatmosphäre habe keinen Einfluß auf die Lichtausbreitung. Die Erde sei eine perfekte Kugel. Die sonnenbeschienene Halbkugel wird dann begrenzt durch einen Großkreis, den Terminator.
Wann die Sonne auf der Erde auf- und untergeht, hängt bekanntermaßen von der Jahreszeit und von der geografischen Breite ab. Das soll hier quantitativ untersucht werden. Dazu wird für einen Breitenkreis der geografischen Breite \(\beta\) berechnet, in welchem geografischen Längenabstand \(\lambda\) vom höchsten Sonnenstand die Sonne auf- bzw. untergeht. Bei einer Rotationsrate der Erde von 15 Grad pro Stunde ergibt sich daraus die Länge des lichten Tages.
Die Tagesdauer ergibt sich breitenabhängig damit geometrisch aus den Schnittpunkten der Breitenkreise mit dem Terminator, also dem Tagesgrenzkreis, an denen die Sonne auf- bzw. untergeht. Diese Schnittpunkte werden hier berechnet.
Als Grundlage dient dazu ein rechtwinkliges Koordinatensystem mit der Ebene der Ekliptik als \(x,y\)-Ebene. In diesem System ist die Erdachse um einen Winkel \(\gamma=\)23.44\(^\circ\) gegen die \(z–\text{Achse}\) geneigt und zwar zur Mittsommerzeit zur Sonne hin, zur Mittwinterzeit zur Gegenseite. Die Erdachse wandert während eines Jahres auf einem Kegelmantel um die \(z\)-Achse. Die \(x\)-Achse sei in Richtung zur Sonne ausgerichtet. Der Terminator schneidet jeden Breitenkreis deshalb bei \(x=\text{0}\), also in der \(y,z\)-Ebene.
Aus der Rotationsgeschwindigkeit der Erde von 360\(^\circ\) in 24 Stunden ergibt sich aus der Differenz der Schnittpunkte die Dauer des lichten Tages oder – komplementär dazu – die Länge der Nacht.
Wäre die Erdachse nicht geneigt sondern hätte die Richtung der \(z\)-Achse, dann wäre ein geografischer Breitenkreis bei einem Erdradius \(R\) gegeben durch \[ \vec{B}_0=R\begin{pmatrix}\cos\beta\cos\lambda\\\cos\beta\sin\lambda\\\sin\beta\end{pmatrix}. \] Bei der tatsächlichen Neigung um den Winkel \(\gamma\) wird ein Breitenkreis zu \begin{align} &\vec{B}≡\begin{pmatrix}B_x\\B_y\\B_z\end{pmatrix} = D_z(\tau)\cdot D_y(\gamma)\cdot D_z(-\tau) \cdot\vec{B}_0 \\ &= R\underbrace{ \begin{pmatrix}\cos\tau&-\sin\tau&0\\\sin\tau&\cos\tau&0\\0&0&1\end{pmatrix}} _{D_z(\tau)}\cdot \underbrace{\begin{pmatrix}\cos\gamma& 0&-\sin\gamma\\0&1&0\\ \sin\gamma& 0&\cos\gamma\end{pmatrix}}_{D_y(\gamma)} \\ & \cdot\underbrace{\begin{pmatrix}\cos\tau&\sin\tau&0 \\-\sin\tau&\cos\tau&0\\0&0&1\end{pmatrix}} _{D_z(-\tau)} \cdot \underbrace{\begin{pmatrix}\cos\beta\cos\lambda\\ \cos\beta \sin\lambda\\\sin\beta\end{pmatrix}}_{\vec{B}_0/R} \end{align}
Die Tagesgrenzen liegen bei \(x=0\). Entsprechend ergibt sich für die \(x\)-Komponente eine Gleichung für \(\lambda\): \begin{align} B_x=&-\cos\tau\sin\beta\sin\gamma\\&-\cos\beta{~\color {magenta}\sin\lambda} \cos\tau\sin\tau\left(1-\cos\gamma \right)\\ &+\cos\beta{\,\color {green}\cos\lambda}\left(\cos\gamma +\sin^2\tau(1-\cos\gamma) \right)\\ &=0. \end{align} Die arctan-Funktion hat immer zwei Werte \(\lambda\), die sich um 180° unterscheiden. Die Tagesgrenzen liegen sich deshalb wie für den Äquator erwartet genau gegenüber, so daß Tag und Nacht dort ganzjährig (also unabhängig von \(\tau\)) je zwölf Stunden dauern.
TEST ------------------ . . . . . . . . . . . . vorige Berechnung:
mit \(c\tau≡ \cos\tau, s\tau≡\sin\tau\) (und entsprechend bei anderen Winkeln)
\begin{align} \tilde{B}/R&=D_z (\tau)\cdot D_y(\gamma)\cdot D_z(-\tau)\cdot\vec{B}_0/R\\ &= \underbrace{ \begin{pmatrix} c\tau&-s\tau&0\\s\tau&c\tau&0\\0&0&1\end{pmatrix}} % Erläuterung _{D_z(\tau)} \underbrace{\begin{pmatrix}c\gamma&0&-s\gamma\\ 0&1&0\\s\gamma&0&c\gamma\end{pmatrix}}_{D_y(\gamma)} \underbrace{ \begin{pmatrix}c\tau&s\tau&0\\ -s\tau&c\tau&0\\0&0&1\end{pmatrix}} % Erläuterung _{D_z(-\tau)} \underbrace{\begin{pmatrix}c\beta {\color {green}c\lambda}\\c\beta {\color {magenta}s\lambda}\\s\beta\end{pmatrix}}_{\vec{B}_0(\lambda)}\\ \end{align}Teilprodukte: \begin{align} D_z(-\tau)\cdot\tilde{B}/R &= \begin{pmatrix} c\tau c\beta {\color {green}c\lambda} +s\tau c\beta {\color {magenta}s\lambda} \\ -s\tau c\beta {\color {green}c\lambda} +c\tau c\beta {\color {magenta}s\lambda}\\ s\beta\end{pmatrix} \\ D_y(\gamma)\cdot D_z(-\tau)\cdot\tilde{B}/R &=\begin{pmatrix} c\gamma c\tau c\beta {\color {green}c\lambda} + c\gamma s\tau c\beta {\color {magenta}s\lambda} -s\gamma s\beta\\ -s\tau c\beta {\color {green}c\lambda} +c\tau c\beta {\color {magenta}s\lambda}\\ s\beta\\ \end{pmatrix}\\ D_z(\tau)\cdot D_y(\gamma)\cdot D_z(-\tau)\cdot\tilde{B}/R &= \begin{pmatrix} c\gamma c\tau^2 c\beta {\color {green}c\lambda} + c\gamma c\tau s\tau c\beta {\color {magenta}s\lambda} -c\tau s\gamma s\beta\\[-2ex] \hspace{-6em}-s\tau^2 c\beta {\color {green}c\lambda} +s\tau c\tau c\beta {\color {magenta}s\lambda}\\ \tilde{B}_y\\\tilde{B}_z \end{pmatrix}\\ \end{align}
\[ \begin{align} \tilde{B_x}/R=&+c\tau^2 c\beta c\gamma {\color {green}c\lambda} +c\gamma c\tau s\tau c\beta {\color {magenta}s\lambda} -c\tau^2 s\tau c\beta {\color {green}c\lambda}\\ & -c\tau s\tau c\beta c\gamma {\color {green}c\lambda}+s\gamma^2 c\beta\\ &-s\tau c\beta {\color {green}c\lambda} +c\tau c\beta {\color {magenta}s\lambda}. \end{align} \]
Mit voriger Rechnung zu vergleichen! ........................
Der Äquator ist ein Großkreis. Unabhängig von seiner Ausrichtung wird er vom Terminator, einem zweiten Großkreis, immer genau zweimal an gegenüberliegenden Punkten geschnitten. Das bietet eine günstige Gelegenheit, die Rechnungen zu erproben. Am Äquator mit \(c\beta≡\cos\beta=1\) ist \begin{align} \tilde{B}_x/R=c\tau^2 c\gamma {\color {green}c\lambda} + c\tau s\tau {\color {magenta}s\lambda} -c\tau^2 s\tau {\color {green}c\lambda}\\ -c\tau s\tau c\gamma {\color {green}c\lambda} + s\gamma^2 - s\tau {\color {green}c\lambda} +c\tau {\color {magenta}s\lambda}. \label{Tagesgrenzen} \end{align} Die Gleichung \( B_x=0\), die an den Tagesgrenzen gilt, hat die Form \[ A\cos\lambda +B\sin\lambda +C=0 \] Ihre Lösung ist von der Art \(\arctan(\text{const})\) und wiederholt sich in Abständen \(\pi\), so daß die Tagesgrenzen sich immer genau gegenüberliegen. Tag und Nacht dauern damit der Anschauung entsprechend je zwölf Stunden.
Mit \( {\color {magenta}s\lambda}=\sqrt{1-{\color {green}c\lambda}^2}\) führt \( B_x=0\) auf eine quadratische Gleichung für die Position \(\lambda\) der Tagesgrenzen, womit dann die Tagesdauer auch bei anderen geografischen Breiten berechnet werden kann.
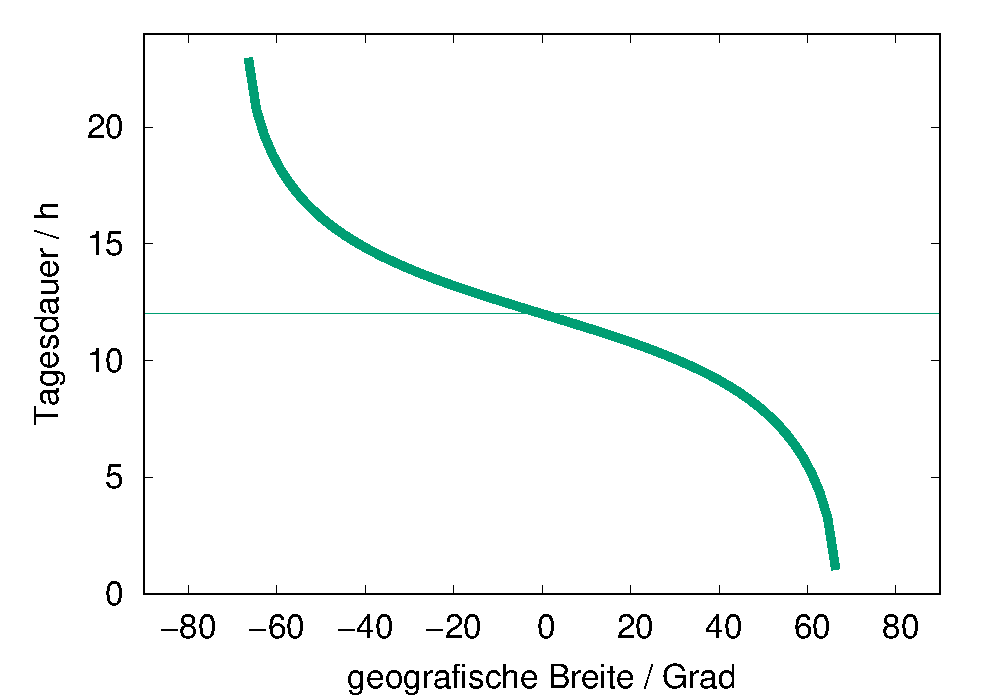
Zur Mittsommerzeit, also bei \(\tau=0, c\tau=1, s\tau=0\) sind auf der Nordhalbkugel bei allen Breiten die längsten Tage zu erwarten. Für die Breitenkreise gilt dann \[ \tilde{\vec{B}} = D_y(\gamma)\cdot\vec{B}_0. \] und die ursprüngliche Gleichung \(B_x=0\) für die Tagesgrenzen vereinfacht sich dann auf \[ \cos\lambda=\tan\beta \tan\gamma \] oder schließlich wie in der folgenden Zeichnung (in Stunden) dargestellt \[ \lambda(\beta)=\arccos(\tan\gamma \tan\beta). \]

Hierbei ermöglicht die Ähnlichkeitstransformation \(D_z(\gamma) \ldots D_z(-\gamma)\) die Achsneigung durch eine einzige Drehung \(D_y(\gamma)\) um die \(y\)-Achse auszudrücken.
Der Terminator ist ein Großkreis bei \(x=0\). In den Schnittpunkten mit dem Terminator ist deshalb auch die \(x\)-Komponente des Breitenkreises \(\vec{B}\) gleich Null. Daraus ergibt sich für einen Breitenkreis bei der Breite \(\beta\) eine nichtlineare Gleichung für die Winkeldifferenz \(\lambda\) zum Mittag als \begin{align} &\underbrace{\cos\tau\cos\gamma\cos\beta}_A~{\color{green}\cos\lambda}\\ &- \underbrace{\cos\tau\sin\gamma\sin\beta}_B\\ &-\underbrace{\sin\tau\cos\beta}_C~{\color {magenta}\sin\lambda} =0. \label{eq:xx3} \end{align} Sie wird mit \(\sin\lambda = \sqrt{1-\cos^2\lambda}\) zu der quadratischen Gleichung für \(\cos\lambda\) \[ \cos^2\lambda -2\,\frac{AB}{A^2+C^2}\,\cos\lambda + \frac{B^2-C^2}{A^2+C^2}=0 \label{eq:xx4} \] mit der Lösung \begin{align} &\cos\lambda(\tau,\gamma,\beta) = \frac{AB}{A^2+C^2}\\ &\pm\sqrt{\left(\frac{AB}{A^2+C^2}\right)^2 - \frac{B^2-C^2}{A^2+C^2} }. \label{eq:clambda} \end{align} Darin ist \(0 \lt\tau\lt \) 360\(^\circ\) der Zeitpunkt im Jahr relativ zur Sommersonnenwende.
Die Gleichung und ihre Lösungen sollen in Spezialfällen überprüft werden.
Zur Zeit der Sonnenwenden, also im Sommer bei \(\cos\tau=1\) und im Winter bei \(\cos\tau=-1\) ist \(\sin\tau=0\). Die Gleichung für \(\cos\lambda\) vereinfacht sich damit zu \[ \cos\lambda=\frac{B}{A}=\tan\gamma\tan\beta \label{eq:lambda1} \] mit den Lösungen als Längendifferenz zum Mittagsmeridian \[ \lambda(\gamma,\beta) = \pm\arccos\left(\tan\gamma\tan\beta\right). \label{eq:lambdaSW} \] Die beiden Vorzeichen ergeben sich wegen der Mehrdeutigkeit der arccos-Funktion.
Gemessen wird, daß die Tageslänge auf den Wendekreisen zwischen 10.5 h und 13.5 h beträgt. Läßt sich das theoretisch bestätigen?
Die oben genannten Koeffizienten der quadratischen
\(\lambda\)-Gleichung werden
an den Wendekreisbreiten zu
\begin{align}
A&=\cos\tau\cos\beta\sin\beta\\ &= \cos\tau\cos\gamma\sin\gamma\\
&= 0.365\text{ bzw. }-0.365\\
B&=-\cos\tau\cos\beta\sin\beta\\ &= -\cos\tau \sin\gamma\cos\gamma=-A\\
C&= -\sin\tau\cos\beta\\&=-\sin\tau\sin\gamma\\&= -0.3978\text{ bzw. }+0.3978
\end{align}
Die beiden Zahlenwerte gelten im Mittsommer
(\(\cos\tau=1\)) bzw. im Mittwinter
(\(\cos\tau=-1\)).
Damit gilt an den Schnittpunkten mit dem Terminator
\begin{align}
AB&=-\cos^2\gamma\sin^2\gamma\\&=-1.332\\
B^2-C^2&= \sin^2\gamma(\cos^2\gamma-1)\\
&=-\sin^4\gamma=-0.02504\\
A^2+C^2&=\sin^2\gamma\left(\cos^2\gamma +1 \right)\\&=0.3932\\
\frac{AB}{A^2+C^2}&=\frac{-(\cos\gamma\sin\gamma)^2}
{\sin^2\gamma\left(1-\sin^2\gamma\right)}\\&=-1,
\end{align}
so daß für Sonnenauf- und -untergang gilt
\begin{align}
\cos\lambda &= \frac{AB}{A^2+C^2}
\left(1\pm\sqrt{1-\frac{(B^2-C^2)(A^2+C^2) }{A^2B^2 }}\right)\\
&=-1\pm \sqrt{\frac{2}{1+\cos^2\gamma}}
\end{align}
Mit der Neigung der Erdachse
um \(\gamma = 23.44°\)
wird damit
\begin{align}
\cos\lambda &= -0.1611\\ \to \lambda&=99.27° \equiv 6.62\text{ h}.
\end{align}
Um diese Dauer weichen Sonnenauf- und -untergang von der Mittagszeit ab.
Der Tag dauert damit 13.24 h.
Dieser Wert liegt nahe bei dem Meßwert von 13.5 h.
Was aber ist mit dem zweiten Meßwert von 10.5 h?
Dies allles muß noch überprüft, mit den Messungen verglichen
und interpretiert werden.
Während der Tag-Nacht-Gleiche gilt \(\cos\tau=0\), \(\sin\tau\pm1\) und damit \(A=0, B=0\) und \(C=\pm\cos\beta\), so daß aus der ersten obigen Gleichung (außer an den Polen bei \(\cos\beta=0\)) wie auch aus ihrer Lösung \(\cos\lambda(\tau,\gamma,\beta)\) folgt \begin{align} &\sin\lambda=0, \cos\lambda=\pm1 \\&\text{und also } \lambda=0,\pm180^\circ. \end{align}
Wäre die Erdachse nicht geneigt, also \(\gamma=0\), dann wäre \(A=\cos\tau\cos\beta\), \(B=0\) und \(C=\sin\beta\cos\beta\). Die quadratische Gleichung für \(\lambda\) lautet damit dann \(\cos^2\lambda =\sin^2\tau\), und die \(x\)-Komponente der Grundgleichungen wäre bereits reduziert auf \(\tan\lambda = 1/\tan\tau\). Mit Hilfe einer über \(\tau\) jahreszeitabhängigen Ähnlichkeitstransformation \((D_z(-\tau) \ldots D_z(\tau))\) kann die Neigung der Erdachse durch eine einfache Drehung \(D_y(\gamma)\) um die \(y\)-Achse berücksichtigt werden. Ein Punkt bei der geografischen Breite \(\beta\) und der Länge \(\lambda\) erhält durch die Folge dieser drei Drehungen die neuen Koordinaten \begin{align} \vec{BK} &= D_z(\tau)\cdot D_y(\gamma)\cdot D_z(-\tau)\cdot \begin{pmatrix}\cos\beta\cos\lambda\\\cos\beta\sin\lambda\\\sin\beta \end{pmatrix}\nonumber\\ &= \begin{pmatrix}\cos\tau&-\sin\tau&0\\\sin\tau&\cos\tau&0\\0&0&1\end{pmatrix}\cdot \begin{pmatrix}\cos\gamma & 0&-\sin\gamma\\0&1&0\\\sin\gamma& 0&\cos\gamma\end{pmatrix}\\ & \cdot\begin{pmatrix}\cos\tau&\sin\tau&0\\-\sin\tau&\cos\tau&0\\0&0&1\end{pmatrix} % \cdot\begin{pmatrix}\cos\beta\cos\lambda\\\cos\beta\sin\lambda\\\sin\beta \end{pmatrix} \nonumber\\ &= \begin{pmatrix} -\cos\tau\sin\beta\sin\gamma-\cos\beta{~\color {magenta}\sin\lambda} \cos\tau\sin\tau\left(1-\cos\gamma \right)\\ %~~~~~~~~~~~~~~~~~~~ +\cos\beta{\,\color {green}\cos\lambda}\left(\cos\gamma +\sin^2\tau(1-\cos\gamma) \right)\\[1ex] % -\sin\beta\sin\gamma\sin\tau +\cos\beta{\,\color {magenta}\sin\lambda}\left(\cos^2\tau+\cos\gamma\sin^2\tau \right)\\[1ex] % \cos\gamma\sin\beta + \cos\beta{\,\color {green}\cos\lambda}\cos\tau\sin\gamma +\cos\beta\sin\gamma{\,\color {magenta}\sin\lambda}\sin\tau \end{pmatrix} \end{align} Ein Schnitt mit dem Terminator bei \(x=0\) für \(\lambda\) auf die nichtlineare Gleichung der Form \[ A\cos\lambda - B - C\sin\lambda =0 \label{eq:BKneuspez} \] mit \begin{align} A &= \cos\beta\left(\cos\gamma+\sin^2\tau(1-\cos\gamma)\right)\label{eq:Aneu}\\ B &= \cos\tau\sin\beta\sin\gamma\\ C &= \cos\beta\cos\tau\sin\tau(1-\cos\gamma)\\ &= \cos\beta\;\frac{\sin(2\tau)}{2}\left(1-\cos\gamma\right) \label{eq:Cneu} \end{align} Sie hat die Lösung (nach WolframAlpha) \[ %\lambda = \arctan\left(\frac{\pm C\sqrt{A^2-B^2+C^2} + AB}{A^2+C^2}\right) \lambda = 2\arctan\left(\frac{\pm\sqrt{A^2-B^2+C^2} - C }{A+B} \right) \label{eq:clambdaneu} \] Wäre die Erdachse nicht geneigt, also \(\gamma=0\), dann wäre \(B=C=0\) und demzufolge nach der dritten der neuen Ausgangsgleichungen jetzt \(\lambda=2\arctan(1)= \pm90^\circ\). Tag und Nacht dauerten dann wie erwartet je zwölf Stunden.
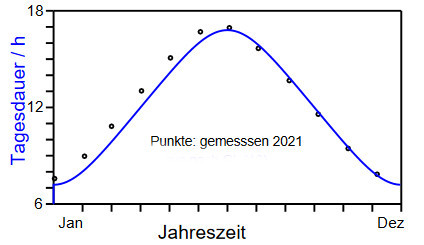
Zu den Sonnenwendezeiten, also bei \(\tau=0\) (Sommer) oder \(\tau=180°\) (Winter), ist \begin{align} \cos\tau&=\pm1, \sin\tau=0,\\ A&=\cos\beta\cos\gamma,\\ B&=\pm\sin\beta\sin\gamma. \end{align} Damit ist breitenabhängig \begin{align} \cos\lambda &= \pm2\arctan\sqrt{\frac{A\mp B}{A\pm B}}\\ &= \pm2\arctan\sqrt{\frac{1\mp\tan\beta\tan\gamma}{1\pm\tan\beta\tan\gamma}}. %= \pm2\arctan\sqrt{0.4739}. \end{align} Z. B. in Hamburg bei der Breite \(\beta=53.6^\circ\) ergibt sich damit für die Tageslänge \begin{align} \lambda&=\pm53.98^\circ\to\\ & 7.19 \text{ h }(\text{Winter) bzw.}\\ & 16.8\text{ h } (\text{Sommer}). \end{align} Das sind 23 bzw. 9 Minuten weniger als die gemessenen Werte 7.57 h bzw. 16.95 h. Dies könnte als atmosphärischer Ausbreitungseffekt gedeutet werden. Die folgende Abbildung zeigt den vollständigen Verlauf der Tagesdauer in Hamburg gemäß der obigen Gleichung für \(\lambda(A,B,C)\) während eines gesamten Jahres.
Am Äquator, also bei \(\beta=0\), ist \(B=0\) und für die geografische Längendifferenz der Tagesgrenze zum Mittagsmeridian folgt damit oder direkt aus der \(x\)-Komponente der Grundgleichungen \begin{align} &\tan\lambda_\text{Äquator} =-\frac{A}{C}\\ &=-\frac{\cos\gamma+\sin^2\tau(1-\cos\gamma)}{\cos\tau\sin\tau(1-\cos\gamma)}. \label{eq:Ae3} \end{align} Mit \(\lambda_\text{Äquator}=\arctan\left(-A/C\right)\) liegt auch auf der Gegenseite bei \(\lambda_\text{Äquator}+180^\circ\), also zwölf Stunden davon entfernt, ein Äquatorpunkt auf dem Terminator. Tag und Nacht dauern dort damit also erfahrungsgemäß immer je zwölf Stunden.
Nord- und Südpol werden in der modifizierte Vektorgleichung für \(\vec{BK}\) wegen \(\cos\beta=0\) zu \[ N,P = \begin{pmatrix}\mp\cos\tau\sin\gamma\\ \mp \sin\tau\sin\gamma\\ \pm\cos\gamma\end{pmatrix}. \] Ein Pol liegt also genau dann auf dem Tagesgrenzgroßkreis, wenn \(\cos\tau=0\), d. h. \(\tau=\pm90^\circ\) ist. Sonnenauf- bzw. -untergang liegen um ein Vierteljahr gegenüber dem sommerlichen Höchststand der Sonne versetzt. An den Polen gibt es also keine täglichen Auf- und Untergänge sondern nur je einen pro Jahr und zwar zur Zeit der Tag-Nacht-Gleiche in den anderen Breiten.
© Günter Green
13-Okt-2021
zu weiteren Physikthemen