Oberfläche einer rotierenden Flüssigkeit

Dieser Text ist noch in Bearbeitung.

Einleitung

In einem zylindrischen Behälter mit senkrechter Achse rotiere eine Flüssigkeit um diese Achse. Um den Mittelpunkt herum entsteht rotationssymmetrisch ein Tal in der Oberfläche. Welche Form nimmt die Oberfläche als Funktion des Abstandes \(r\) zur Drehachse an?

Auf die Flüssigkeit wirkt neben der senkrechten Schwerkraft außerdem wegen der Rotation die Fliehkraft im rechten Winkel zur Achse. Die Flüssigkeitsoberfläche stellt sich im rechten Winkel zur Gesamtkraft beider Kräfte ein. Andernfalls würde eine Kraftkomponente parallel zur Oberfläche nämlich eine Verschiebung zur Folge haben.

Die Schwerkraft, das Gewicht \(G\), darin wirkend auf ein Tröpfchen der Masse \(m\), ist in einem Gefäß der geringen Höhe \(h\) konstant gleich \[ G = m g. \] Die Fliehkraft \(F\) hängt jedoch vom radialen Abstand \(r\) vom Drehmittelpunkt ab: \[ F(r) = m r w(r)^2. \] Sie ist proportional zur Winkelgeschwindigkeit \(w(r)\) in der rotierenden Flüssigkeit, die vom radialen Achsabstand \(r\) abhängen kann.

Die Summe \(\vec{R}\) aus Gewicht und Fliehkraft ist ein Vektor mit Komponenten in \(x\)-Richtung, einer Richtung im rechten Winkel zur Rotationsachse und in \(z\)-Richtung, der Richtung der senkrechten Rotationsachse. Er ist \[ \vec{R}=m\begin{pmatrix} rw^2(r)\\g \end{pmatrix} \] und bildet mit der \(z\)-Achse einen Winkel \(\psi(r)\) mit \[ \tan\psi(r)=\frac{g}{rw^2(r)}. \] Wenn man den Schnitt der Flüssigkeitsoberfläche mit der \(x\)-\(z\)-Ebene schreibt als \[ y(r)=y_0+ y'(r)\;r \text{ mit der Steigung } y'(r), \] dann ist \[ y'(r)=-\frac{1}{\tan\psi(r)}=-\frac{rw^2(r)}{g} \] zu wählen, damit die Oberfläche im rechten Winkel zur Gesamtkraft bleibt.

Es lassen sich verschiedene Fälle unterscheiden:

Die Rotationswinkelgeschwindigkeit \(w\) ist bei allen radialen Achsabständen \(r\) gleich\(\;w_0\). Entsprechend ist dann überall die Fliehkraft \(F(r)\) auf eine Masse \(m\) gleich \(m r w^2\), und die Flüssigkeitsoberfläche formt sich als \[ y(r)= y_0 + \int\limits_{0}^{r}y'(r) \text{ d}r= y_0 - \frac{w^2_0}{g}\frac{r^2}{2}. \]

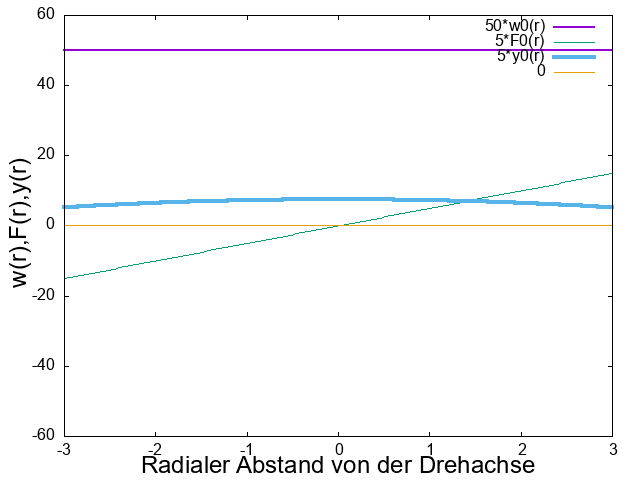
Abbildung 1:
Winkelgeschwindigkeit \(w(r)=w_0\) in rotierender Flüssigkeit ohne Abbremsung an der Gefäßwand. Die Winkelgeschwindigkeit \(w(r)=w_0\) erscheint als waagerechte Gerade, die Fliehkraft \(F(r)\) als geneigte Gerade und das Flüssigkeitsniveau \(y(r)\) als nach unten geöffnete schwach gekrümmte Parabel.
Es stellt sich also ein Rotationsparaboloid ein.
Durch Reibung an der Gefäßwand kann die Winkelgeschwindigkeit dort abgebremst werden. Die Winkelgeschwindigkeit der rotierenden Flüssigkeit hängt dann vom radialen Abstand etwa folgendermaßen von der Drehachse ab: \[ \omega(r) = w_0\left(1-\text{e}^{k\left(r-R \right)} \right), \]

Damit wird die Fliehkraft \[ F(r)= mrw_0^2\left(1-\text{e}^{k\left(r-R \right)} \right)^2 \]

und \begin{align} \tan\psi(r) &= \frac{F(r)}{G}\\ &= r \frac{w_0^2\left(1-\text{e}^{k\left(r-R \right)} \right)^2}{g}. \end{align} Die Flüssigkeitsoberfläche erhält damit die Form \[ y(r) = y_0 -\left(\frac{g}{r w^2\left(1 -\text{e}^{k\left(r-R \right)} \right)}\right) \]

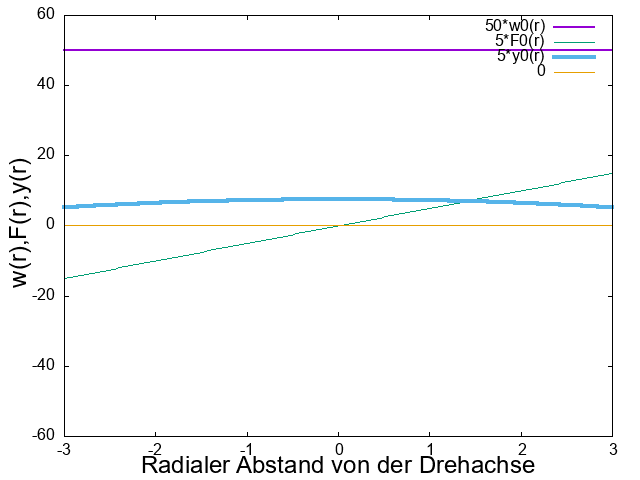
Abbildung 2:
Die Winkelgeschwindigkeit \(w(r)=w_0\) in rotierender Flüssigkeit mit Abbremsung an der Gefäßwand ist jetzt keine waagerechte Gerade mehr, sondern neigt sich bei Annäherung an die Gefäßwand nach unten. Demzufolge verformt sich der Verlauf der Fliehkraft \(F(r)\) ähnlich.