Schräger Wurf

Einleitung

Ein Körper (Ball oder Geschoß) der Masse \(m\) werde am Ort \[ \vec{r}_0= \begin{pmatrix}0\\0\end{pmatrix} \] mit der Anfangsgeschwindigkeit \[ \vec{v}_0 =v_0\begin{pmatrix}\cos\alpha\\\sin\alpha\end{pmatrix} =\frac{\text{d}\vec{r}_0}{\text{d}t} =\begin{pmatrix}\dot{x_0}\\\dot{z_0}\end{pmatrix} \] schräg nach oben geschossen. Seine Flugbahn soll bestimmt werden, aus der sich Gipfelhöhe, Reichweite und Flugdauer ergeben.

Herleitung

Nach Abschuß in der Höhe \(z=z_0=0\) zur Zeit \(t=t_0=0\) gilt für den Körper der Masse \(m\) wegen der Impulserhaltung \begin{align} &m\,\frac{\text{d}^2\vec{r}}{\text{d}t^2} = m\vec{g} \end{align} mit \[ \vec{r}(t)=\begin{pmatrix} x)t)\\y(t)\end{pmatrix}~\text{ und }~ \vec{g}=\begin{pmatrix}0\\-g\end{pmatrix} \] und entsprechend \begin{align*} \frac{\text{d}\vec{r}}{\text{d}t} &=\vec{g}t \\ \vec{r}(t)&=\frac{\vec{g}}{2}\,t^2+\vec{v}_0 t \end{align*} bzw. komponentenweise \begin{align*} \ddot{x}(t)&= 0 ~~\to~~ \dot{x}(t)=v_{x,0}\\ &\to {x}(t) = \dot{x}_0 t\\ \ddot{z}(t)&=-g ~~\to~~ \dot{z}(t)= -g t+v_{z,0}\\ &~~\to~~z(t) = -\frac{g}{2}(t-t_0)^2+\dot{z}_0 (t-t_0). \end{align*} Im Maximum der Bahn ist \[ \dot{z}= -gt+\dot{z}_0=0. \] Es wird erreicht zur Zeit \[ t_{\text{max}}= \frac{\dot{z}_0}{g} \] bei \[ x_{\text{max}}=\dot{x}_0 t_{\text{max}}= \frac{\dot{x}_0\dot{z}_0}{g} \] und hat dort die Höhe \[ z_{\text{max}}= \frac{\dot{z}_0^2}{2g}. \] Danach fällt der Körper zurück und erreicht die Ausgangshöhe \(z_0=0\) zur Zeit \[ t_1 = \frac{2\dot{z}_0}{g} =2 \,t_{\text{max}}. \]

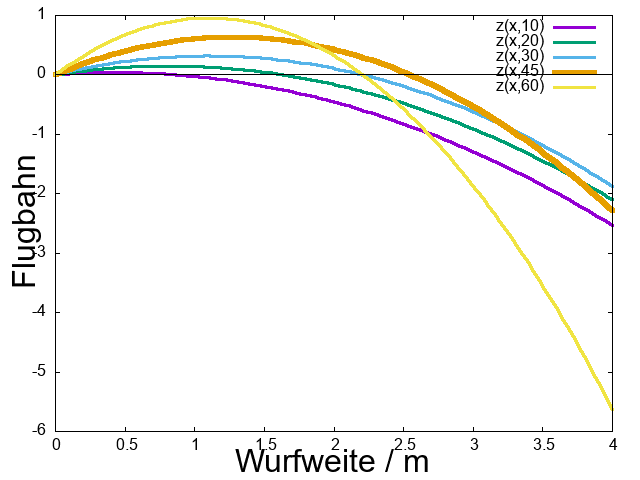
Abbildung 1: Ein Körper werde bei \(x=0\) mit einer Abfluggeschwindigkeit \(v_0\) unter verschiedenen Winkeln, nämlich 10°, 20°, 30°, 45° und 60° schräg aufwärts geworfen bzw. geschossen. Auf einer Parabelbahn erreicht er nach dem Maximum wieder die Abflughöhe mit der größten Wurfweite bei 45°.

bei \begin{align} x_1 = \frac{2\dot{z}_0}{g}\dot{x}_0 &=\frac{2v_0^2}{g} \cos\alpha \sin\alpha\\ &= \frac{v_0^2}{g}\sin(2\alpha). \end{align} Die Reichweite hängt also vom Winkel \(\alpha\) ab, unter dem die Bahn begonnen wird. Am weitesten fliegt der Körper, wenn als Abflugwinkel \(\alpha=45^\circ\) gewählt wird, so daß \(\sin(2\alpha)=1\) ist. Damit ergibt sich die größte Reichweite als \[ x{_1}_\text{max}=\frac{v_0^2}{g}. \] Bei einer Abfluggeschwindigkeit \(v_0=1\) m/s käme der Körper damit etwa 10 cm weit.

Umgekehrt ließe sich aus einer empirisch ermittelten maximalen Reichweite \(x_\text{1max}\) eines Körpers seine Abflugeschwindigkeit \[ v_0 = \sqrt{g x_\text{1max}} \] berechnen.