Information

Da es den Begriff Information bereits in der normalen Umgangssprache gibt, sollte seine Definition mit der gewohnten Bedeutung im Einklang bleiben. In diesem Sinne definieren wir qualitativ:

Information ist das, was wir nicht wissen.

Diese – scheinbar vielleicht überraschend klingende – Definition sagt, daß das, was wir schon wissen, für uns keine Information mehr ist. Sie macht Information weiterhin zu einem subjektiven Begriff. Wir werden also nicht danach fragen, wieviel Information objektiv etwa in einer Nachricht steckt, sondern wieviel darin für uns subjektiv neu ist. Das kann für verschiedene Menschen unterschiedlich viel sein, und hängt für ein und denselben Menschen davon ab, wie genau er die Nachricht schon vorher gekannt hat.

Zur quantitativen Definition von Information betrachten wir einen Versuch, der zwei mögliche Ausgänge hat und dessen Ausgang wir nicht vorhersagen können. Wir nehmen also an, daß beide Versuchsausgänge für uns gleichwahrscheinlich seien. Als Beispiel können wir uns das Werfen einer Münze vorstellen, bei dem wir nicht wissen, ob die Münze Vorder- oder Rückseite zeigen wird. Die Menge an Information, die uns ein solcher Versuch liefert, erklären wir zur Maßeinheit der Information:

Der Informationsgehalt eines Versuchs mit zwei gleichwahrscheinlichen Ausgängen beträgt 1 bit.

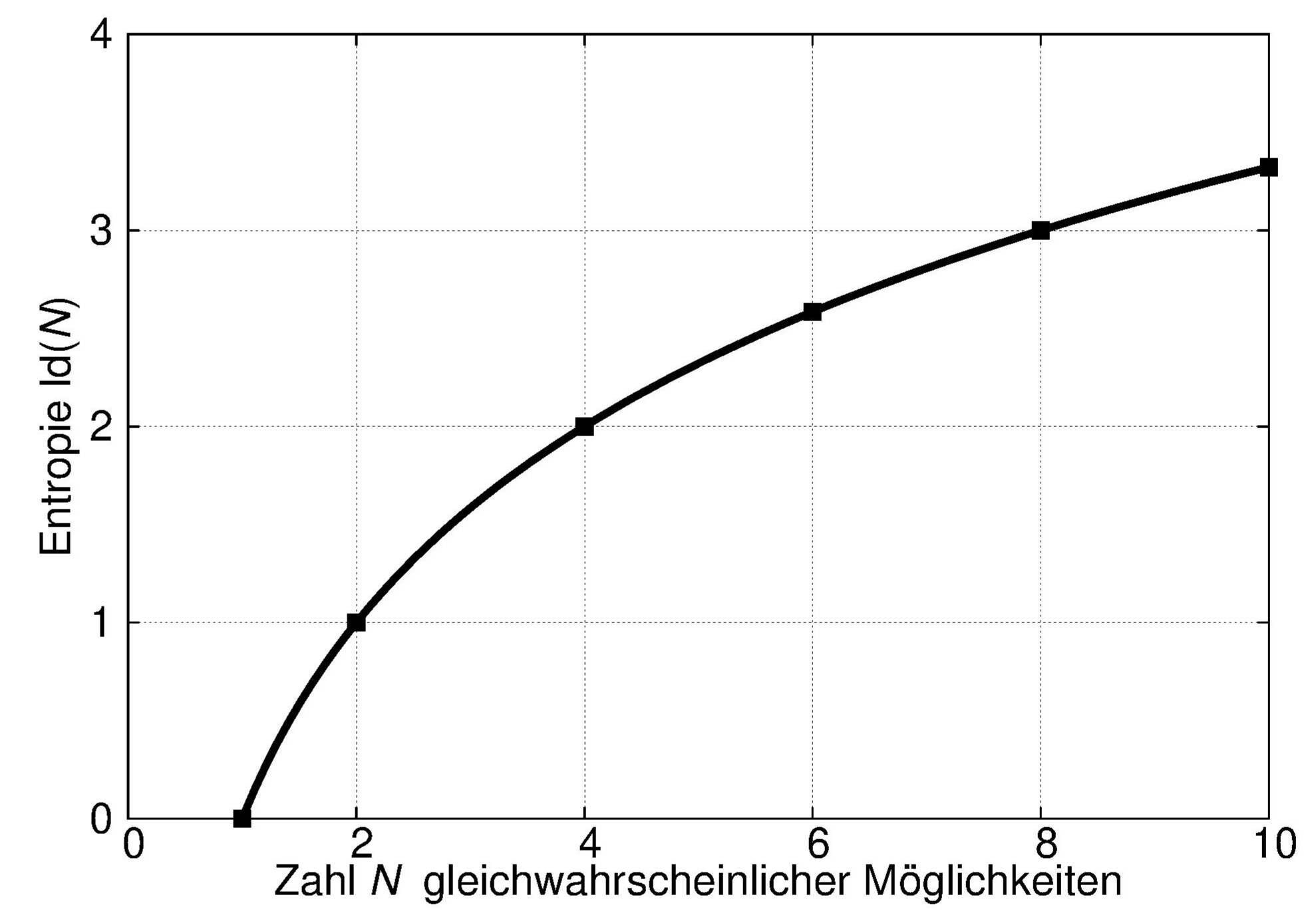
Der Anwendungsbereich dieser Definition läßt sich leicht erweitern. Nehmen wir an, ein Versuch habe N = 2ⁿ gleichwahrscheinliche Ausgänge. Wir können sie in zwei gleich große Mengen aufteilen und den Experimentator dann fragen, ob der Versuchsausgang in der ersten oder der zweiten Hälfte liegt. Da beide Hälften gleichwahrscheinlich sind, erfragen wir damit ein erstes Bit an Information. Die betroffene Hälfte unterteilen wir ebenso und erfragen ein weiteres Bit. So fahren wir fort, bis die letzte Frage uns genau einen der Ausgänge angibt. Wir haben dann

I = n = ld N

bit an Information erfragt. Hierin ist ld der Logarithmus zur Basis 2.

Zwischen dem Logarithmus dualis ld x und dem leichter zugänglichen Logarithmus naturalis ln x besteht der Zusammenhang

ld x = ln x ld e = ln x / ln 2

Man findet dies, indem man x, geschrieben als

x = 2^{ld x} = e^{ln x}

zur Basis 2 oder zur Basis e logarithmiert (ln 2 ≅ 0.6931, ld e = 1/ln 2 ≅ 1.4427).

Die nächste, naheliegende Verallgemeinerung besteht darin, die obige Gleichung auch auf die Fälle anzuwenden, in denen N keine Zweierpotenz ist. Im allgemeinen erhält man dann kein ganzzahliges Vielfaches eines Bit als Informationsgehalt mehr. Das (nur) logarithmische Anwachsen ist in der folgenden Abbildung dargestellt.

Um die Größe der Informationseinheit Bit zu veranschaulichen:
Beim Zahlenlotto '6 aus 49' gibt es \[ N = {49\choose6}=13 \,983\, 816 \] gleichwahrscheinliche Möglichkeiten, 6 Zahlen aus 49 auszuwählen. Folglich ist der Informationsgehalt einer solchen Auswahl \[ I_6 = \text{ld}{49\choose6}\approx 23.73 \text{ bit}. \]

Information und Wahrscheinlichkeit

Die Wahrscheinlichkeit jedes von N gleichwahrscheinlichen Versuchsausgängen ist p = 1/N. Der Informationsgehalt I in bit eines solchen Versuchs, ausgedrückt durch die Wahrscheinlichkeiten seiner möglichen Ausgänge, ist somit \[ I = \text{ld}\left(\frac{1}{p}\right) = -\text{ld } p . \] Diese Form bietet die Möglichkeit, die Definition des Informationsgehaltes auch auf Versuche mit N nicht gleichwahrscheinlichen Ausgängen x_i zu verallgemeinern. Die Wahrscheinlichkeiten der Versuchsausgänge seien \(p(x_i) \equiv p_i \) mit \[\sum_{i=1}^N p_i=1\] Der Versuchsausgang x_i hat dann den Informationsgehalt \[ I(x_i)= -\text{ld } p_i. \] Je unwahrscheinlicher der Versuch ausgeht, um so höher ist also der Informationsgehalt.

Der so definierte Informationsgehalt z. B. einer Auswahl eines Zeichens aus einem Zeichensatz ist also ausschließlich durch die Statistik, also durch Wahrscheinlichkeiten, nicht aber durch die Semantik, d. h. die Bedeutung der Zeichen, bestimmt.

Entropie

Im Mittel über alle seine möglichen Ausgänge x_i, die mit den Wahrscheinlichkeiten p_i auftreten, liefert ein Versuch X die Information

\[ H(X)= \sum_{i=1}^N p_i I(x_i) = -\sum_{i=1}^N p_i \text{ ld }p_1. \] Man nennt den mittleren Informationsgehalt H(X) eines Versuchs seine Entropie (Shannon 1948). Sie kann wie Information in bit gemessen werden und ist ein Maß dafür, wie viel Neues, Unvorhersagbares etwa ein Versuch dem Experimentator oder ein Kunstwerk dem Betrachter im Mittel liefert. Die Entropie ist bestimmt durch die Entscheidung des Beobachters, welche Versuchsausgänge er in Betracht ziehen und unterscheiden will und welche Wahrscheinlichkeiten er ihnen zuordnet.

Wie der Informationsgehalt I(x_i) ist damit also auch die Entropie ein subjektiv geprägter Begriff. Durchführungen des Versuchs können für den Experimentator die Wahrscheinlichkeiten ändern. Er lernt dann, den Ausgang besser vorherzusagen, und die Entropie nimmt, wie wir formal noch sehen werden, für ihn ab.

Bei N möglichen Versuchsausgängen ist die Entropie eine Funktion der N Wahrscheinlichkeiten p_i. Wegen der Normierung verbleiben N−1 Freiheitsgrade.

Ein Beispiel:

Wie viel Entropie steckt in der Frage 'Wie viele Richtige sind bei einem Lottotip im Spiel '6 aus 49' zu erwarten?'

Die Wahrscheinlichkeit, genau k Richtige zu haben, ist \[ p_k = \frac{\displaystyle{6\choose k}{{49-6}\choose{6-k}}}{{\displaystyle49\choose \displaystyle6}} \] Die Wahrscheinlichkeiten p_k und ihre Beiträge zur Entropie sind in der folgenden Tabelle zahlenmäßig aufgeführt.

k	p_k	−p_k ld(p_k)
0	0.4359649	0.5223
1	0.4130194	0.5268
2	0.132378	0.3862
3	0.0176504	0.1025
4	9.68619 •10^-4	0.0097
5	1.84498 •10^-5	0.00029
6	7.15112 •10^-8	0.0000017

Am wahrscheinlichsten ist es also, überhaupt keine Zahl richtig vorhergesagt zu haben. Im Mittel ist die Zahl der Richtigen \[ \overline{k} = \sum_{k=0}^6 p_k\,k \approx 0.73. \] Aus der rechten Spalte der Tabelle ergibt sich eine Entropie von \[ H = -\sum_{k==}^6 p_k \text{ ld }p_k \approx 1.548 \text{ bit}. \] Dies ist nur gut halb so viel wie bei sieben gleichwahrscheinlichen Möglichkeiten. Zwar liefern, wie definierende Gleichung zeigt, sehr unwahrscheinliche Versuchsausgänge, wenn sie auftreten, sehr viel Information. Sie tragen aber vernachlässigbar wenig zum mittleren Informationsgehalt, also zur Entropie bei. Es ist daher völlig unkritisch, solche Ausgänge bei der entropiemäßigen Bewertung eines Versuchs außer acht zu lassen.

Bei einem Versuch mit zwei möglichen Ausgängen ist die Entropie wegen der Normierung der Wahrscheinlichkeit gleich \[\large H(X) = -p\text{ ld } p - \left(1-p\right)\text{ ld}\left(1-p\right) \equiv S(p), \] also eine Funktion von nur einer Variablen.

Man nennt S(p) die Shannon-Funktion. Sie hat, wie auch die Abbildung zeigt, die Eigenschaften \[ \large\begin{align} S(1-p)&=S(p)\\ S(0) &=0\\ S(p_{max}) &= 1, p_{max}=1/2 \\ \frac{\partial S}{\partial p} &= \pm \infty \text{bei} p=1 \text{ oder } 2 \end{align} \]

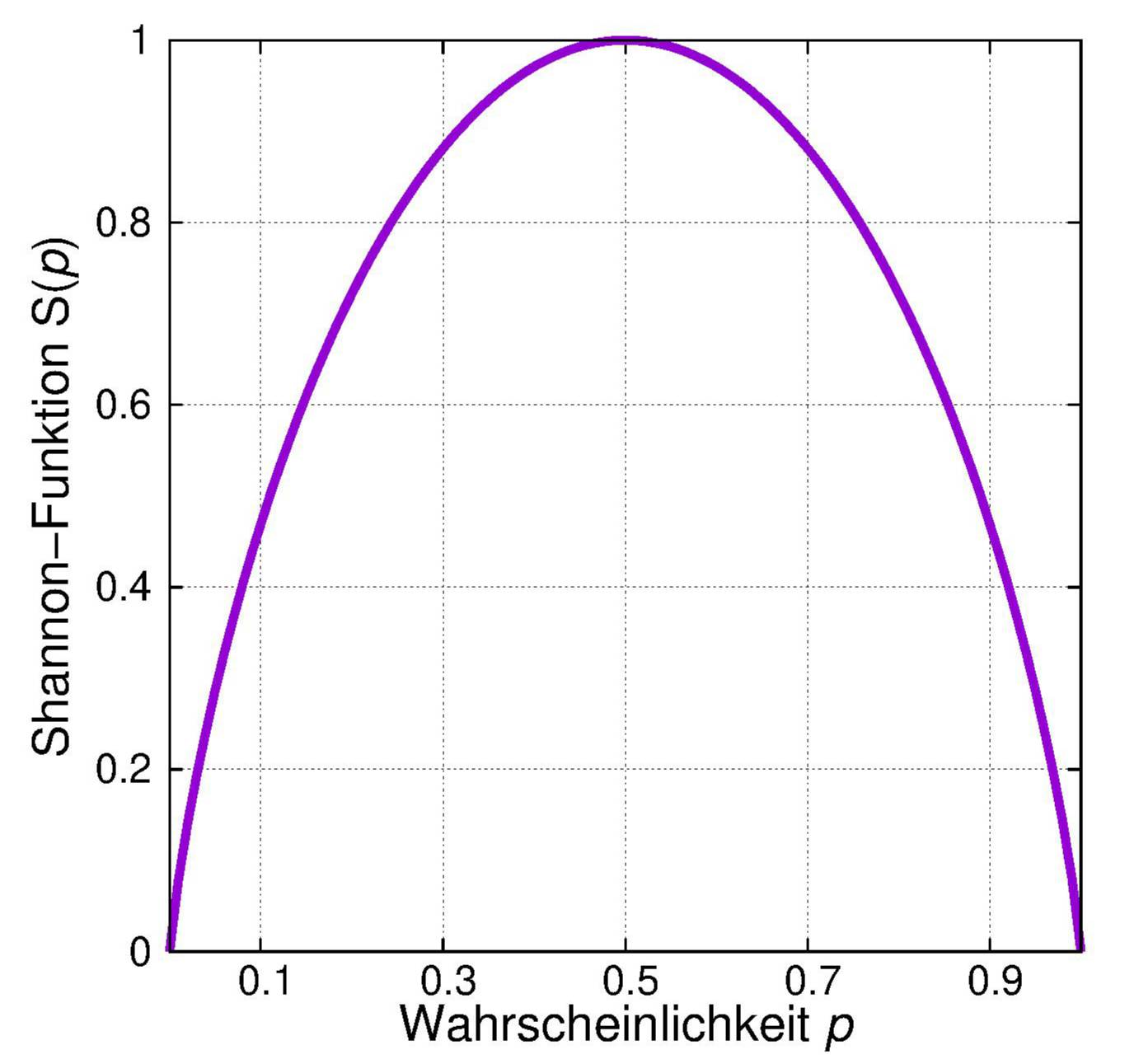
Die zweite dieser Gleichungen erhält man nach der Regel von de l'Hospital.

Hier in der Form

anzuwenden.

Die Entropie ist also Null, wenn das Ergebnis mit Sicherheit vorhersagbar ist, und am größten, wenn die Versuchsausgänge gleichwahrscheinlich sind.

Dies gilt auch für Versuche mit mehr als zwei Ausgängen. Auch dann können wir den Satz aussprechen:

Die Entropie eines Versuches X mit den möglichen Ausgängen x_i ist dann am größten, wenn alle Ausgänge gleichwahrscheinlich sind.

Beweis nach Fano:

Wir werden hier und in anderen Beweisen die Ungleichung

verwenden.
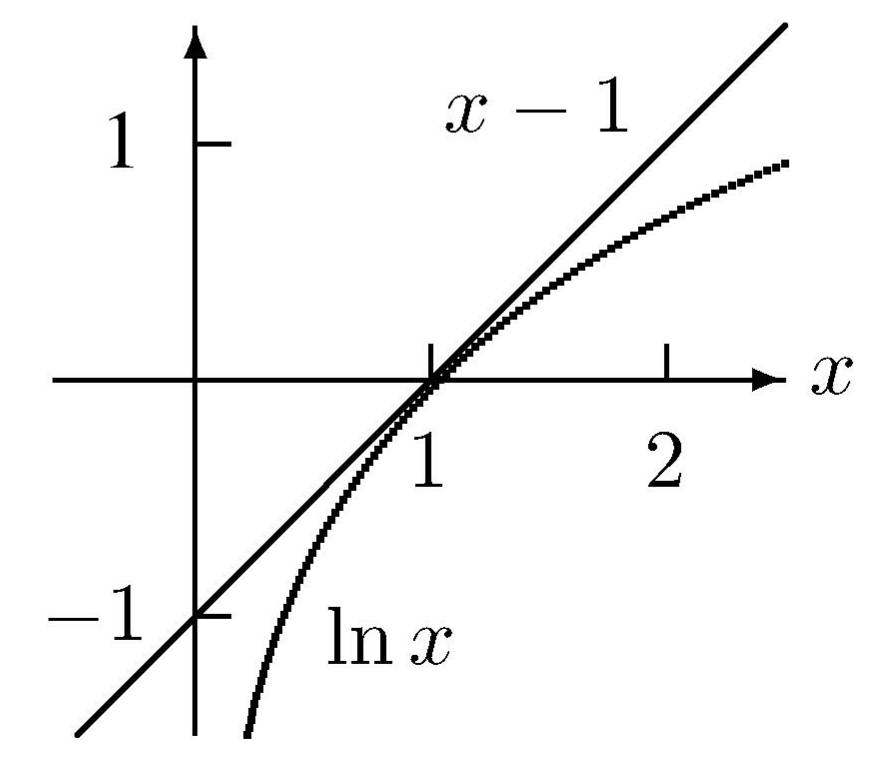
Das Gleichheitszeichen gilt offensichtlich, wenn x = 1 ist. Für alle anderen positiven x ist y(x) := ln x − x+1 negativ, denn die erste Ableitung y'(x)=(1-x)/x verschwindet nur für x = 1, und die zweite Ableitung y''(x) = −1/x^2 ist dort negativ, so daß y(x) dort sein einziges Maximum mit dem Wert Null hat
Wir zeigen, daß

ist. Es gilt nämlich

=
≤
=

Das Gleichheitszeichen gilt genau dann, wenn das Argument des Logarithmus gleich Eins ist, d. h. wenn

für alle Versuchsausgänge gleich groß ist, q. e. d.

Nach dem Prinzip der maximalen Entropie (Jaynes, 1957) gilt die Umkehrung dieses Satzes, daß nämlich, wenn außer der Normierung keine weiteren Einschränkungen für die Wahrscheinlichkeiten bestehen, sie für maximale Entropie alle gleich groß sein müssen.

Auch bei mehr als zwei möglichen Versuchausgängen ist die Entropie dann Null, wenn einer von ihnen mit Sicherheit, also mit der Wahrscheinlichkeit Eins auftritt und die die anderen die Wahrscheinlichkeit Null haben.

Als Maß für die Unvorhersagbarkeit eines Versuches stellt die Entropie den Wert eines Versuchs dar. Je kleiner nämlich seine Entropie ist, um so sicherer kann man seinen Ausgang vorhersagen und um so eher kann man auf seine Durchführung verzichten.

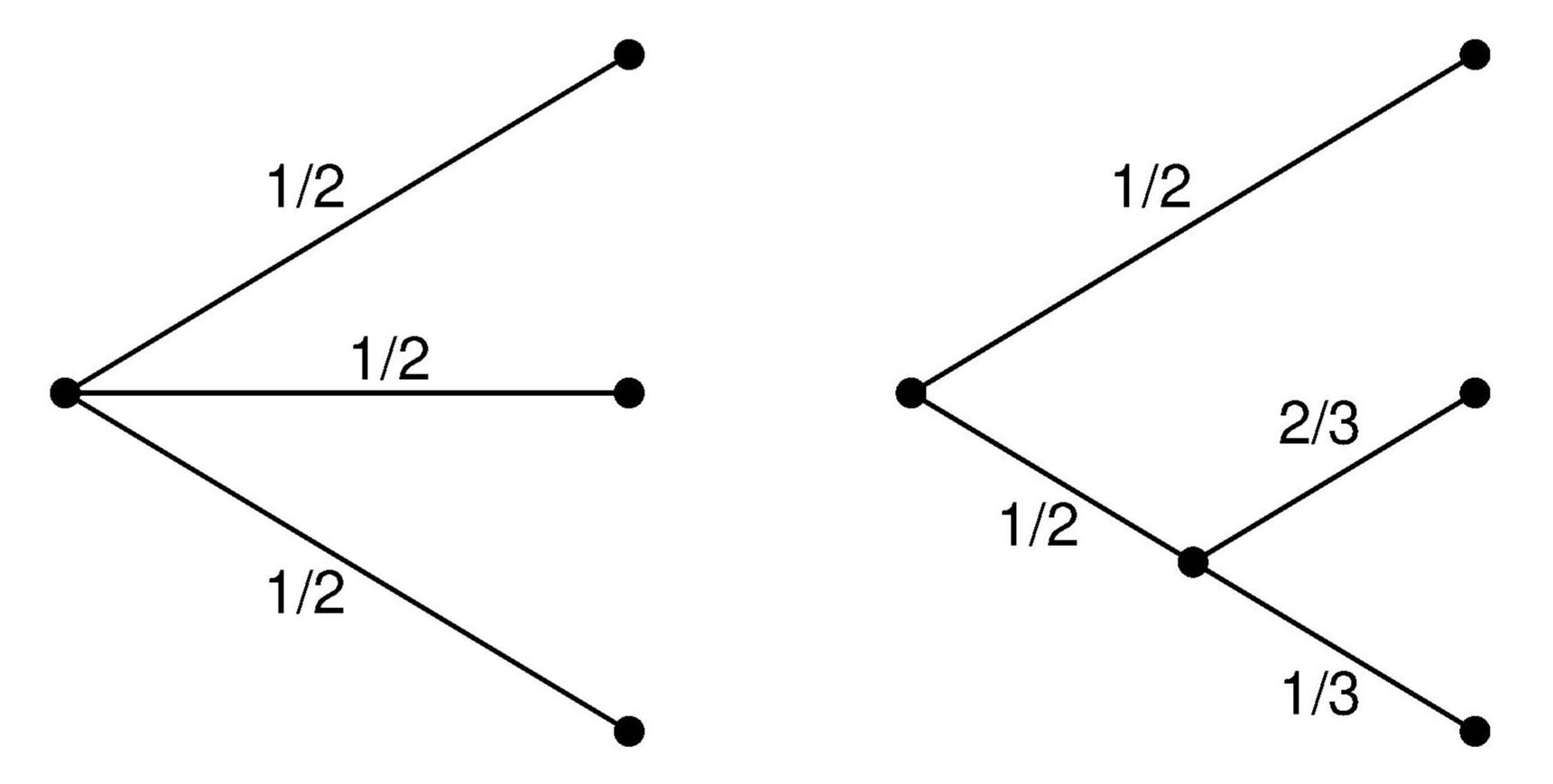
Formal kann man die Entropie eines Versuchs durch die folgenden drei Eigenschaften definieren:

Die Entropie hängt stetig von den Wahrscheinlichkeiten p_i ab.
Bei gleichwahrscheinlichen Ausgängen nimmt sie mit der Zahl der Ausgänge zu.
Zerlegt man eine Entscheidung zwischen mehreren Möglichkeiten in Teilentscheidungen, so ist die gewichtete Summe der Entropien der Teilentscheidungen gleich der Entropie der ursprünglichen Entscheidung.

Die Shannonsche Entropie

ist – bis auf die Konstante k, die die Informationseinheit festlegt – die einzige Funktion mit diesen drei Eigenschaften (Shannon, 1948).


	=
	≤
	=