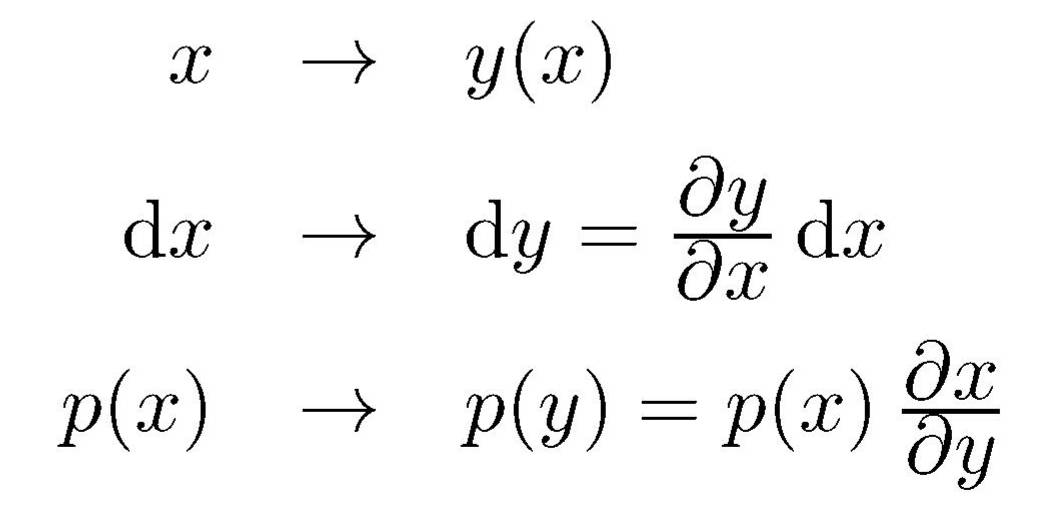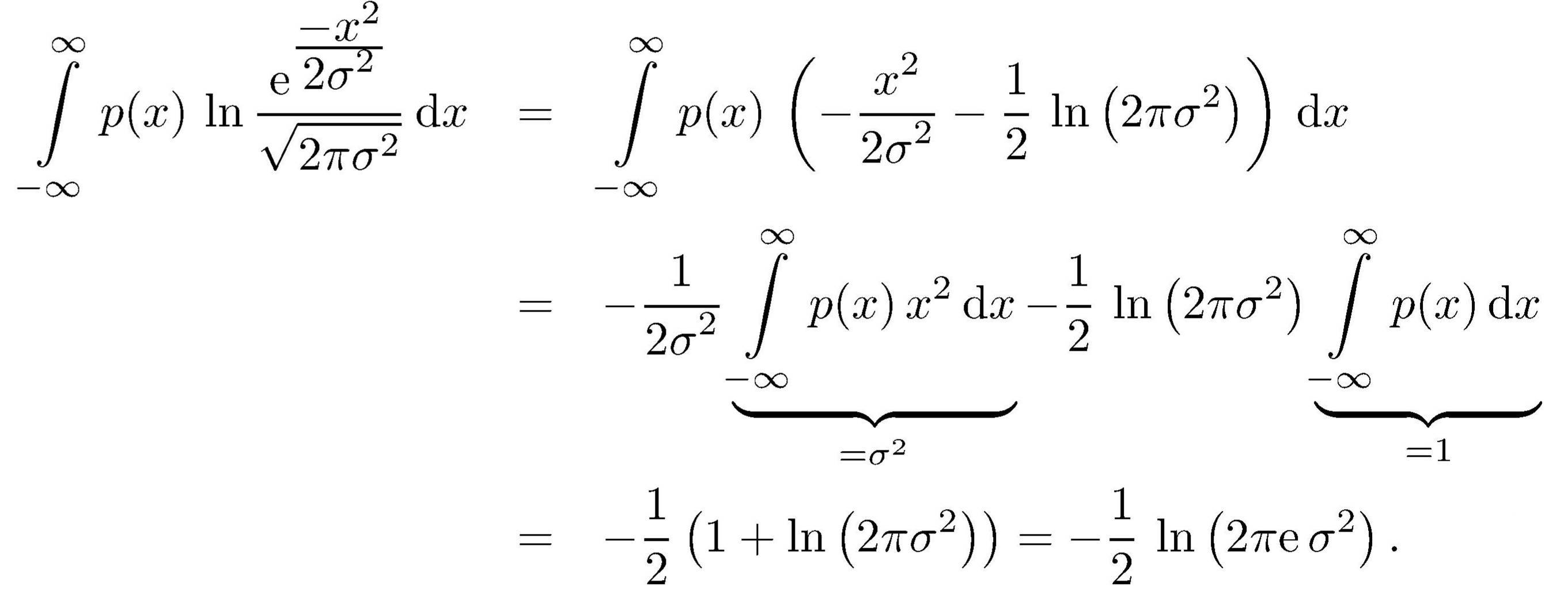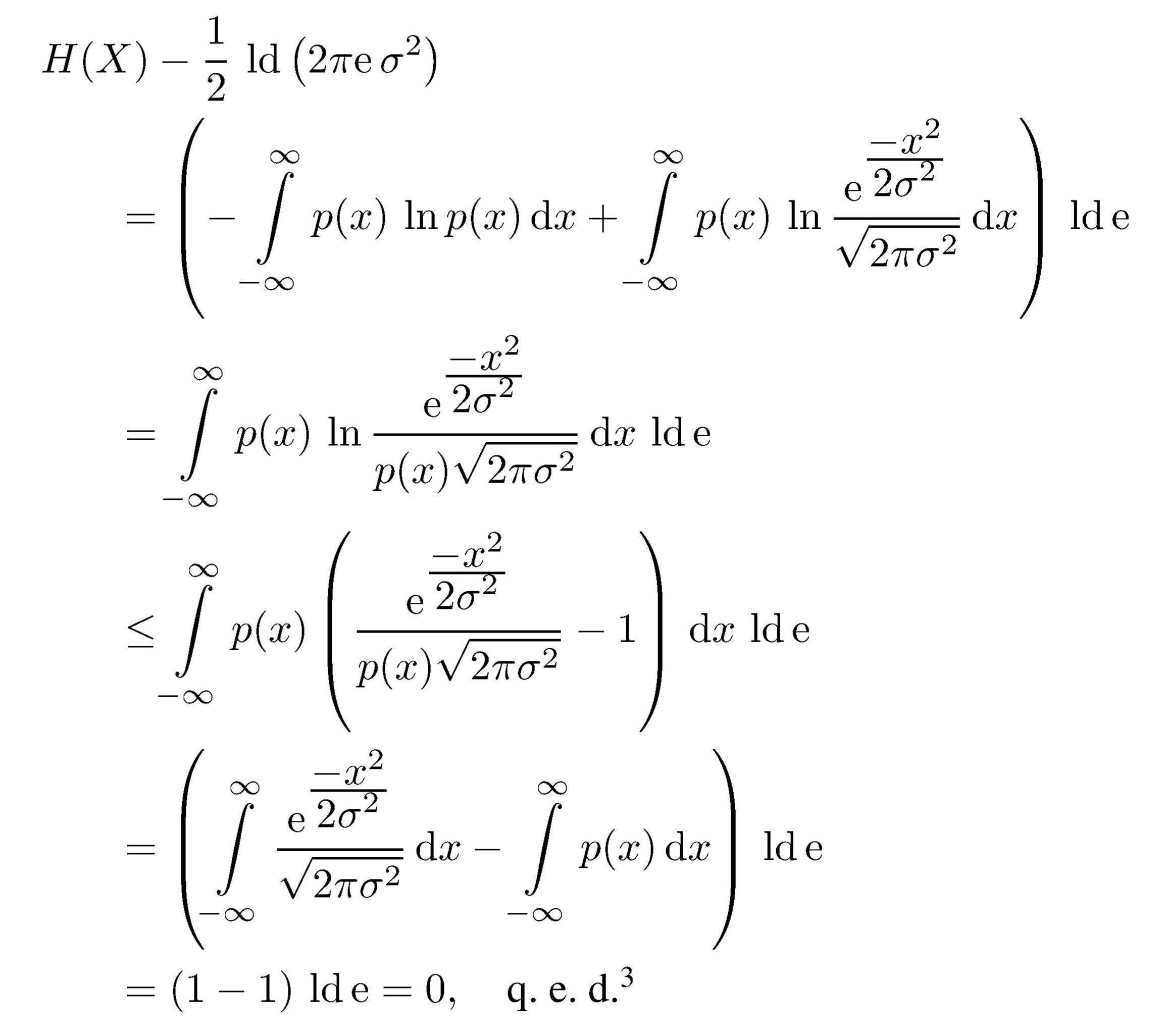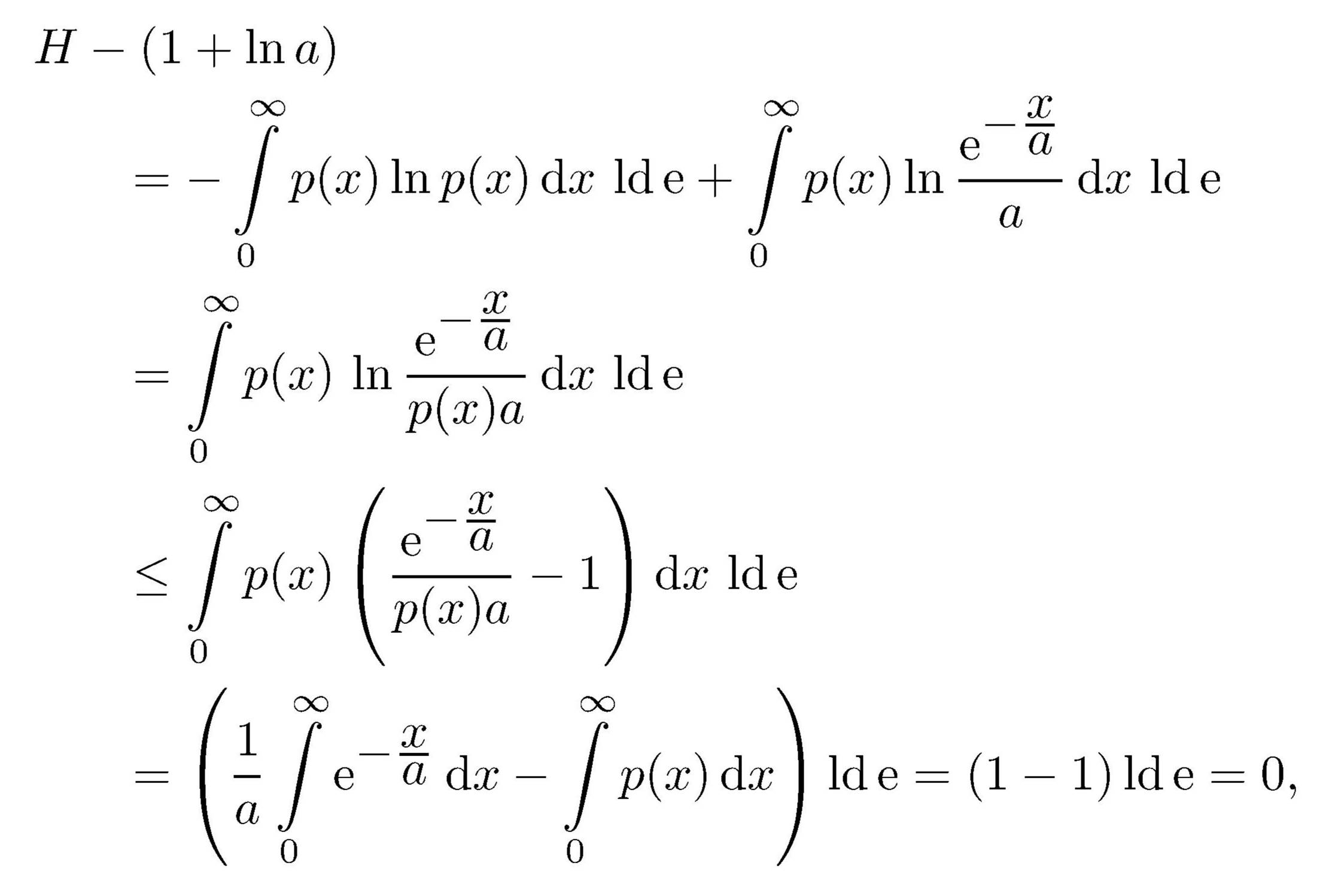Entropie bei kontinuierlichen Verteilungen
Wenn ein Versuch X Ausgangswerte x liefert, die kontinuierlich verteilt liegen,
dann ist ihre Verteilung durch eine Wahrscheinlichkeitsdichte p(x) zu beschreiben.
Die Wahrscheinlichkeit, ein Ergebnis zwischen x und x+dx zu erhalten, ist
dann p(x) dx.
Als Entropie definieren wir jetzt
Hierin seien x und p(x ) dimensionslos.
Die Entropie diskreter Verteilungen hat bei völliger Bestimmtheit
(p(xi) = 0 für alle i bis auf eins) den Minimalwert Null.
Im Gegensatz dazu kann die Entropie kontinuierlicher Verteilungen auch negativ werden.
Nehmen wir z. B. eine rechteckige Verteilung der Höhe 1/ε an,
die sich von −ε/2 bis ε/2 erstreckt (und also auf Eins normiert ist),
dann ist ihre Entropie

Sie wird negativ, sobald ε kleiner als Eins wird.
Die Entropie hängt im kontinuierlichen Fall offenbar vom Koordinatensystem ab.
Wählt man die Skala des Koordinatensystems so, daß ε gleich Eins wird, dann ist H(X) gleich Null.
Wenn die Rechteckbreite ε dem im realen Fall
immer endlichen Auflösungsvermögen einer Messung entspricht,
dann ist ein solches Koordinatensystem
mit seiner Einheit an die Meßgenauigkeit angepaßt,
und die Entropie ist wie im diskreten Fall nichtnegativ.
Der völligen Bestimmtheit bei diskreten Verteilungen entspricht hier die
Festlegung auf eine Intervall der Größe der Auflösung.
Ein Koordinatensystem, das in dieser Weise gleichmäßig für alle x-Werte
des Meßbereichs an die Meßgenauigkeit angepaßt ist, könnte als das
natürliche Koordinatensystem der Messung bezeichnet werden.
Ein Wechsel des Koordinatensystems braucht sich nicht auf lineare Streckungen
der Koordinatenachsen zu beschränken, sondern kann von allgemeinerer Form sein.
Er sollte aber durch eine umkehrbar eindeutige Transformation geschehen, da sonst Information verlorengeht.
Mit den Abbildungen
bleibt für beliebige Grenzen a und b das Integral
und damit die Normierung der Wahrscheinlichkeit erhalten.
Eine in x-Koordinaten gegebene Entropie Hx
transformiert sich hierbei
in die Entropie
Hy verschiebt sich also um einen durch die Art der Koordinatentransformation bestimmten
konstanten additiven Betrag.
Beispiel:
In einem Meßbereich von A bis B sei p(x) konstant gleich 1/(B−A).
Wir wenden eine logarithmische Transformation
an.
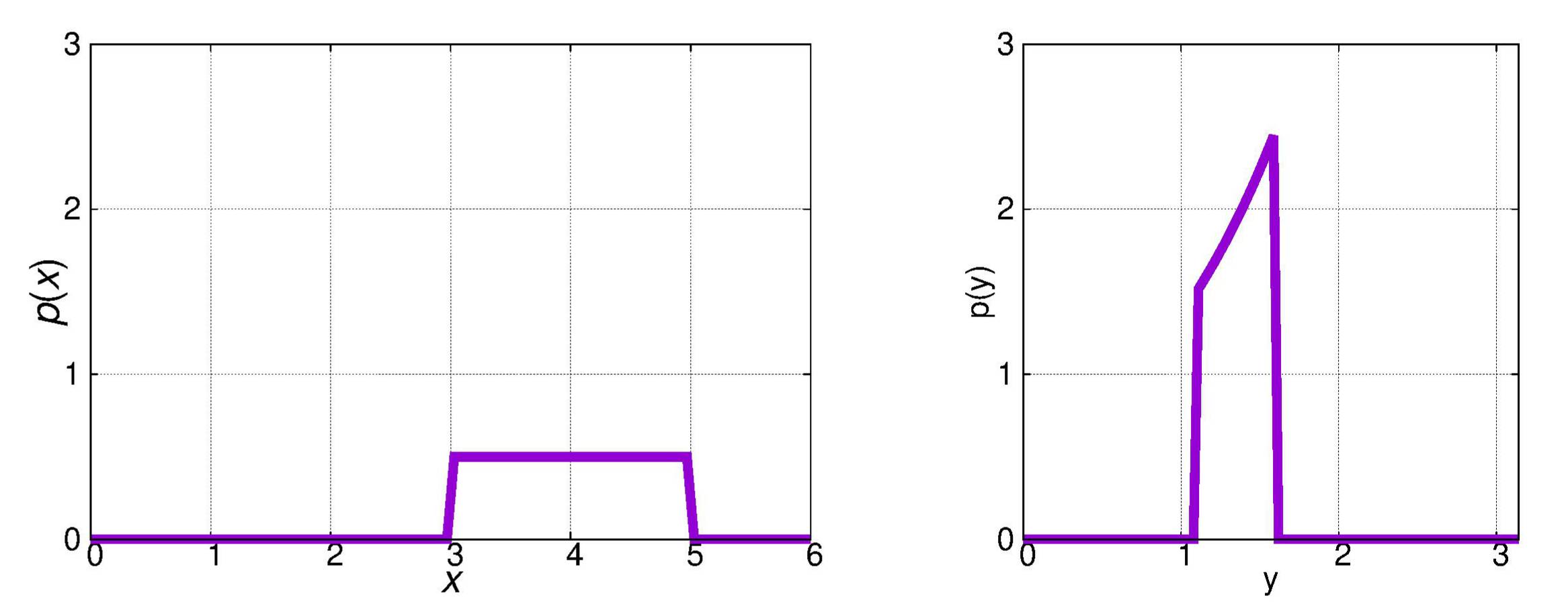
Aus einer rechteckigen Verteilung p(x) wird dann eine im zugehörigen
y-Meßbereich exponentiell ansteigende Verteilung p(y).
Beide Verteilungen sind in der Abbildung gegenübergestellt.
Die Entropie ist im linken Bild
Beim rechten Bild erhalten wir
Bei mehrdimensionalen Koordinatentransformationen, wenn x und y also als Vektoren zu verstehen sind,
ist ∂x/∂y durch die Jacobische Funktionaldeterminante
zu ersetzen.
Entropien transformieren sich damit in der Weise
Als konkretes Beispiel sei der Übergang von kartesischen zu Polarkoordinaten
in der Ebene gezeigt. Es sei also
Die Jacobi-Determinante ist
und somit p(r,φ) = r p(x,y).
Damit ergibt sich für die Entropie
Die Entropie ändert sich also um einen additiven Term,
nämlich den Mittelwert des Logarithmus der Funktionaldeterminante.
Der Logarithmus ist Null bei reinen Drehungen, also linearen Transformationen,
deren Jacobi-Determinante gleich Eins ist.
Bei Differenzen von Entropien, wie sie z. B. bei der noch zu behandelnden
Übertragung von Information über Nachrichtenkanäle eine Rolle spielen wird,
heben sich diese additiven Terme gegenseitig auf, so daß die Wahl des
Koordinatensystems dann ohne Einfluß bleibt.
Ein Beispiel für eine kontinuierliche Verteilung:
Ist s eine dimensionsbehaftete Größe, dann können wir durch
x := s / s0
eine dimensionslose Größe x einführen.
Im Intervall [x1,x2] sei die Wahrscheinlichkeitsdichte gleich
1 / (x2 − x1)
und sonst gleich Null.
Dann ist die Entropie
Wir können s0 als die Größe von Quantisierungsstufen auffassen.
Die Entropie eines Versuchs, dessen Ergebnisse in einem gewissen Meßbereich
gleichwahrscheinlich verteilt liegen, hängt dann logarithmisch davon ab,
wie groß der Meßbereich ist und in wie viele Stufen man ihn einteilt.
Der Entropie sind dabei im allgemeinen technische Grenzen gesetzt.
Weder läßt sich ein beliebig großer Meßbereich noch – aus Gründen der Stabilität und Linearität –
eine beliebig feine Quantisierung erreichen.
Bei Digitalvoltmetern etwa, die einen Analog-Digital-Wandler (ADC) enthalten,
ist die Quantisierung erkennbar vorgegeben und angepaßt an die Meßgenauigkeit.
Bei Analoginstrumenten wie etwa einem Drehspulvoltmeter ist die Quantisierung
nicht vorgegeben.
Sie und damit die Entropie einer Messung mit einem Analoginstrument
ergeben sich aber aus dessen Ablese- und der Eichgenauigkeit.
Der Quantisierung entspricht ein Fehler
dx = ds / s0
in der Messung.
In dem eben beschriebenen Beispiel ist der absolute Wert dieses Fehlers im gesamten Meßbereich gleich groß.
Gelegentlich ist es erwünscht, den relativen Quantisierungsfehler
innerhalb des Meßbereichs konstant zu halten.
Die kleinen Meßwerte sollen dann also absolut genauer als die großen erfaßt werden.
Das ist durch eine logarithmische Abbildung der dimensionsbehafteten Meßwerte s
auf dimensionslose Zahlen x gemäß
zu erreichen.
Nehmen wir wie vorher eine Gleichverteilung der Wahrscheinlichkeit
zwischen x1 und x2 an,
dann ergibt sich jetzt als Entropie der Messung
Wegen der logarithmischen Abbildung ist jetzt
dx = k ds / s.
Ein einheitlicher absoluter Quantisierungsfehler dx
entspricht also einem einheitlichen relativen Fehler in der Meßgröße s.
Zur Entropie tragen die Feinheit k der Quantisierung,
also die Stufenzahl, und der Dynamikbereich s2/s1 bei.
Beispiel:
Der Dynamikbereich s2/s1 sei 5000,
und der zulässige relative Quantisierungsfehler Δs/s sei 1 Prozent.
Dann ist (wegen Δx = 1) k gleich 100 zu setzen, und die Entropie der Messung wird
H(X) = ld(100 ln(5000)) ≅ 9.73 bit.
Zum Vergleich:
Bei linearer Quantisierung müßte die Einteilung beim kleinsten Meßwert in
Zellen der Größe s1/100 über den gesamten Bereich fortgesetzt werden.
Man erhielte dann 100 s2/s1 Zellen entsprechend einer Entropie
H(X) = ld 500 000 ≅18.93 bit, die also fast doppelt so
groß wäre wie im logarithmischen Fall.
Bei Messungen mit diskreten möglichen Ergebnissen ist, wie wir gesehen hatten,
die Entropie dann am größten und damit die Vorhersagbarkeit am kleinsten,
wenn alle Ergebnisse gleich wahrscheinlich sind.
Wie sieht dies bei Messungen mit kontinuierlich verteilten Ergebnissen aus?
Eine Gleichverteilung in einem unendlichen Bereich würde
wegen der Normierung der Gesamtwahrscheinlichkeit
eine unendlich kleine Wahrscheinlichkeitsdichte erfordern.
Eher von praktischem Interesse wäre etwa ein beidseitig begrenzter Meßbereich
oder ein zwar unbegrenzter Meßbereich,
bei dem die Meßwerte jedoch anderen Einschränkungen unterliegen.
So könnte man zum Beispiel den Mittelwert der Energie der Meßwerte,
die proportional zu x2 ist, vorgeben durch
Dann gilt, wie gleich bewiesen wird, für die Entropie
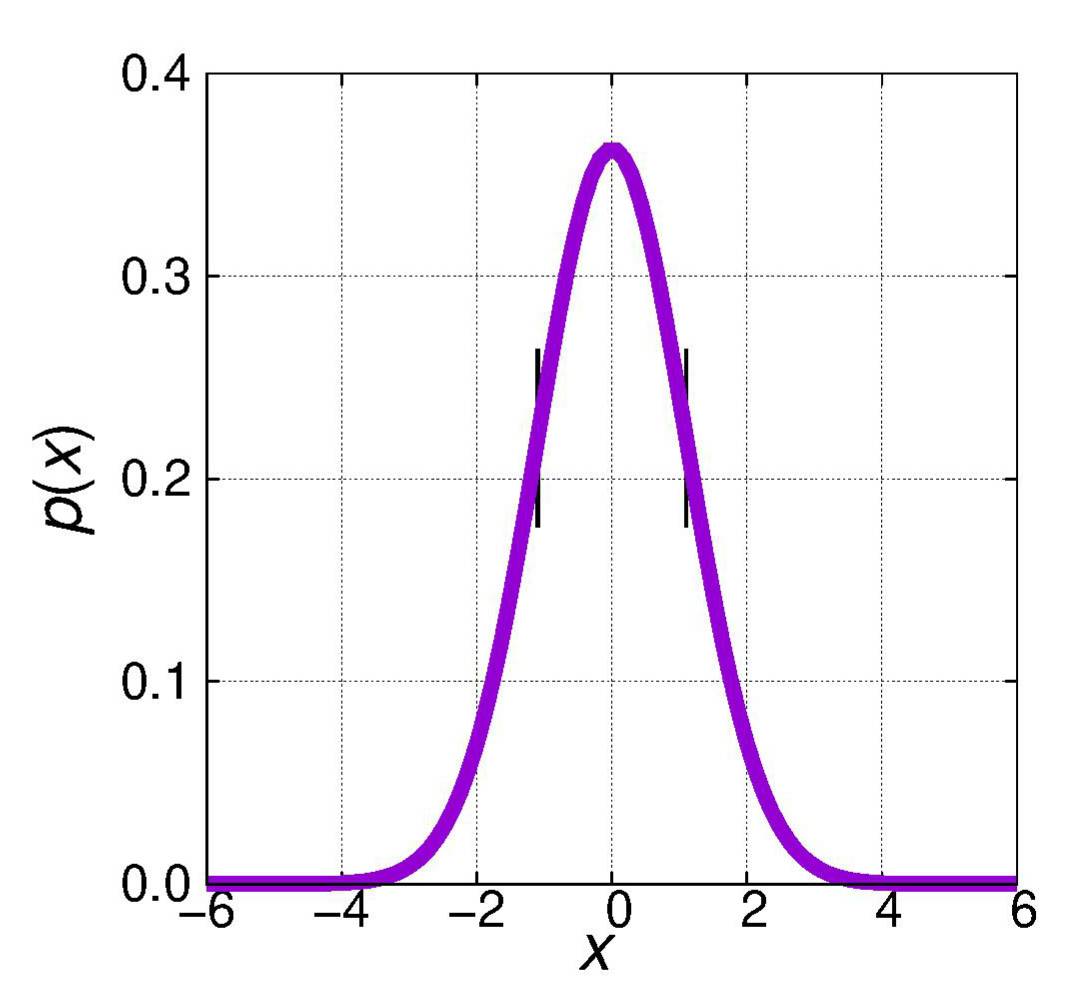
Hinreichend dafür, daß sie ihren Maximalwert annimmt, ist,
daß die Wahrscheinlichkeit eine normierte Gauß-Verteilung ist, d. h.
Zum Beweis
(siehe Fano,1966) verwenden wir die Beziehung
Aus ihr folgt – unter Verwendung der Ungleichung ln x ≤ x − 1
Das Integral über die Gauß-Kurve
erhält man z.\,B. mit
x =
r cos(φ
und
y =
r sin(φ) aus
Das Gleichheitszeichen gilt ) genau dann,
wenn das Argument des Logarithmus gleich Eins ist, d. h. wenn p(x), wie oben behauptet,
eine normierte Gauß-Verteilung mit der Streuung σ ist.
Auch hierzu werden wir im nächsten Abschnitt die Umkehrung beweisen,
nämlich daß für maximale Entropie unter der Bedingung (\ref{eq:gauss1})
die Wahrscheinlichkeit notwendigerweise gaußverteilt sein muß.
Bei anderen Nebenbedingungen benötigt man auch andere Wahrscheinlichkeitsverteilungen für maximale Entropie.
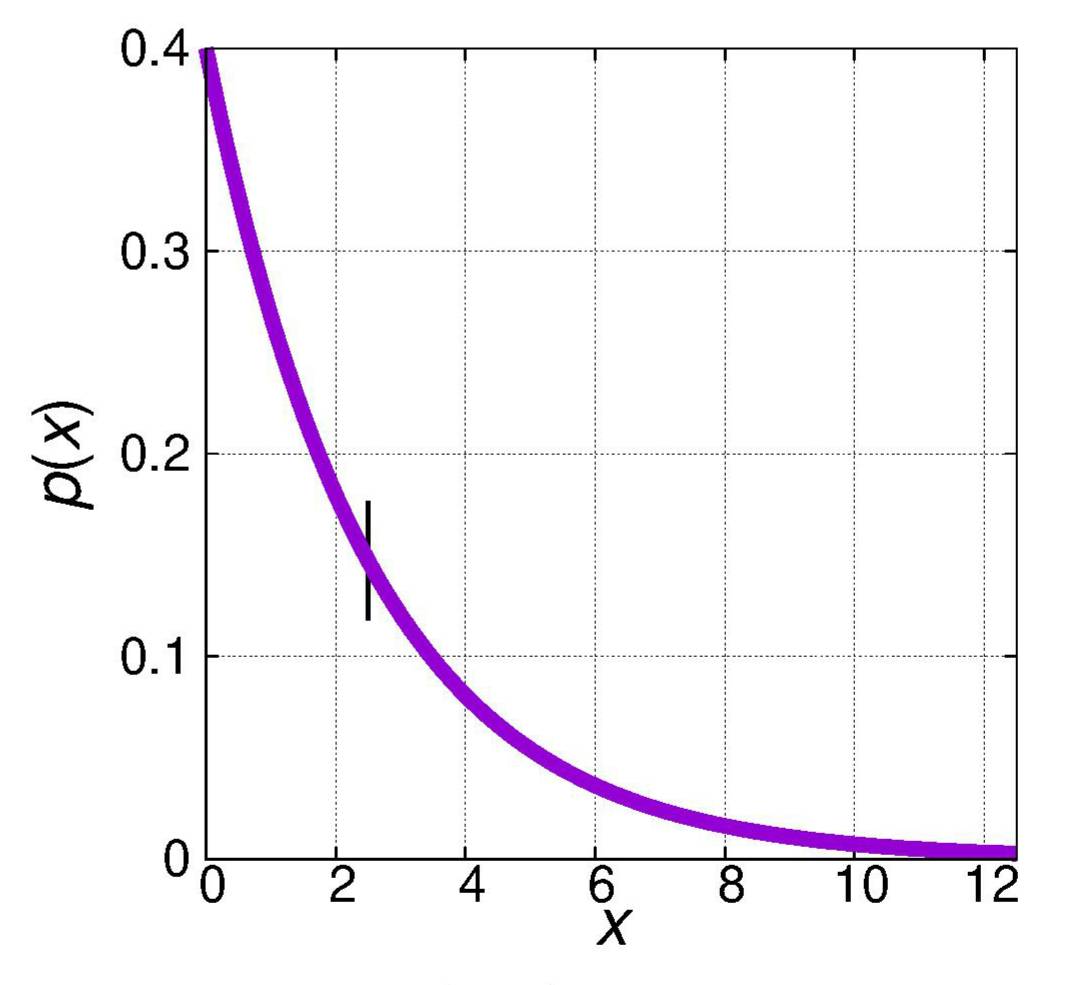
Nehmen wir z. B. eine einseitige normierte Verteilung p(x)
mit der Nebenbedingung (hier für den Mittelwert von x
statt wie vorher von x2)
Vorbereitend finden wir hier
Damit ergibt sich analog zum vorhergehenden Fall
womit gezeigt ist, daß unter der Normierungsbedingung
eine bei x = 0 sprunghaft beginnende exponentiell abklingende Verteilung
maximale Entropie ergibt.
© Günter Green
zurück
weiter
zurück zum Anfang
22
-Sep-2018