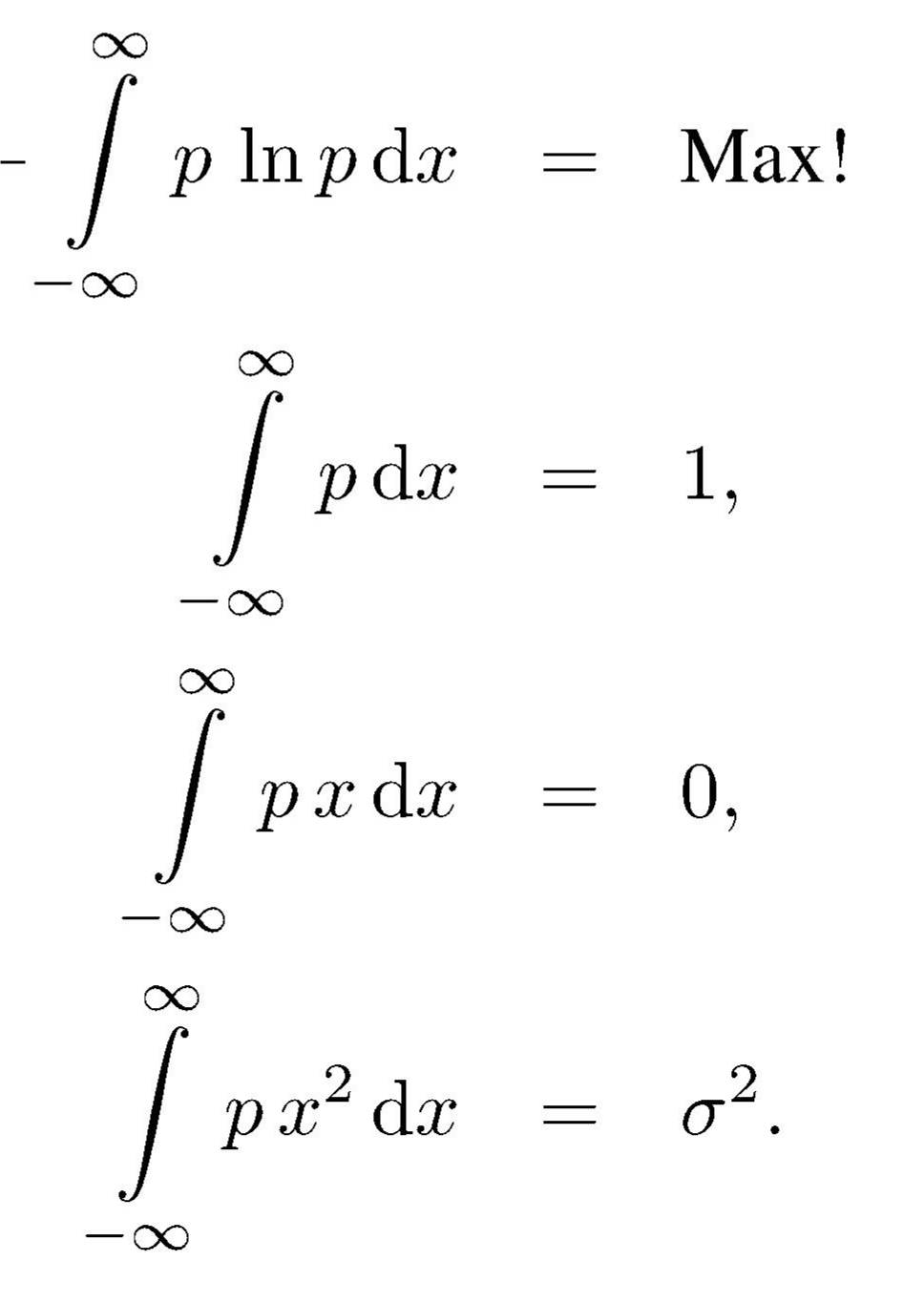Informationstheorie

Beispiele für das Prinzip der maximalen Entropie

Realer Würfel:

Wenn jeder Wurf mit Sicherheit eine der sechs Augenzahlen liefert, gilt für deren Wahrscheinlichkeiten p_i

Bekannt sei aus einer – nicht notwendigerweise großen – Zahl von Würfen als einziges eine mittlere Augenzahl

Unter dieser Nebenbedingung ist nach den Wahrscheinlichkeiten p_i für das Auftreten der Augenzahl i beim nächsten Wurf gefragt.

Es liegt also ein lineares Gleichungssystem aus nur zwei Gleichungen zur Bestimmung der sechs Unbekannten p_i vor. Ohne das Prinzip der maximalen Entropie wäre dieses Problem als nicht eindeutig lösbar anzusehen, denn die Lösung hätte vier freie Parameter.

Eine wichtige Methode, Wahrscheinlichkeitsverteilungen nach dem Prinzip der maximalen Entropie zu bestimmen, bedient sich der Variationsrechnung: Wir definieren ein zu maximalisierendes Funktional J, in das die Nebenbedingungen mit Lagrange-Multiplikatoren λ_k eingefügt sind:

Die Variation des Funktion als nach einem Variationsparameter α, von dem die gesuchten Wahrscheinlichkeiten in beliebiger Weise abhängen mögen, ist im gesuchten Maximum gleich Null:

Hinreichend und wegen der beliebigen α-Abhängigkeit auch notwendig dafür ist, daß die Klammer gleich Null ist, d. h.

Die Werte der Lagrange-Multiplikatoren λ_k erhalten wir aus den Nebenbedingungen, deren Zahl ja mit der der Multiplikatoren übereinstimmt. Wegen der Normierung läßt sich λ₀ durch λ₁ ausdrücken, und es ergibt sich

Die obige Nebenbedingung liefert

Die maximale Entropie läßt sich wegen der Nebenbedingung und der daraus folgenden Gleichung für p_i in der Form

berechnen.

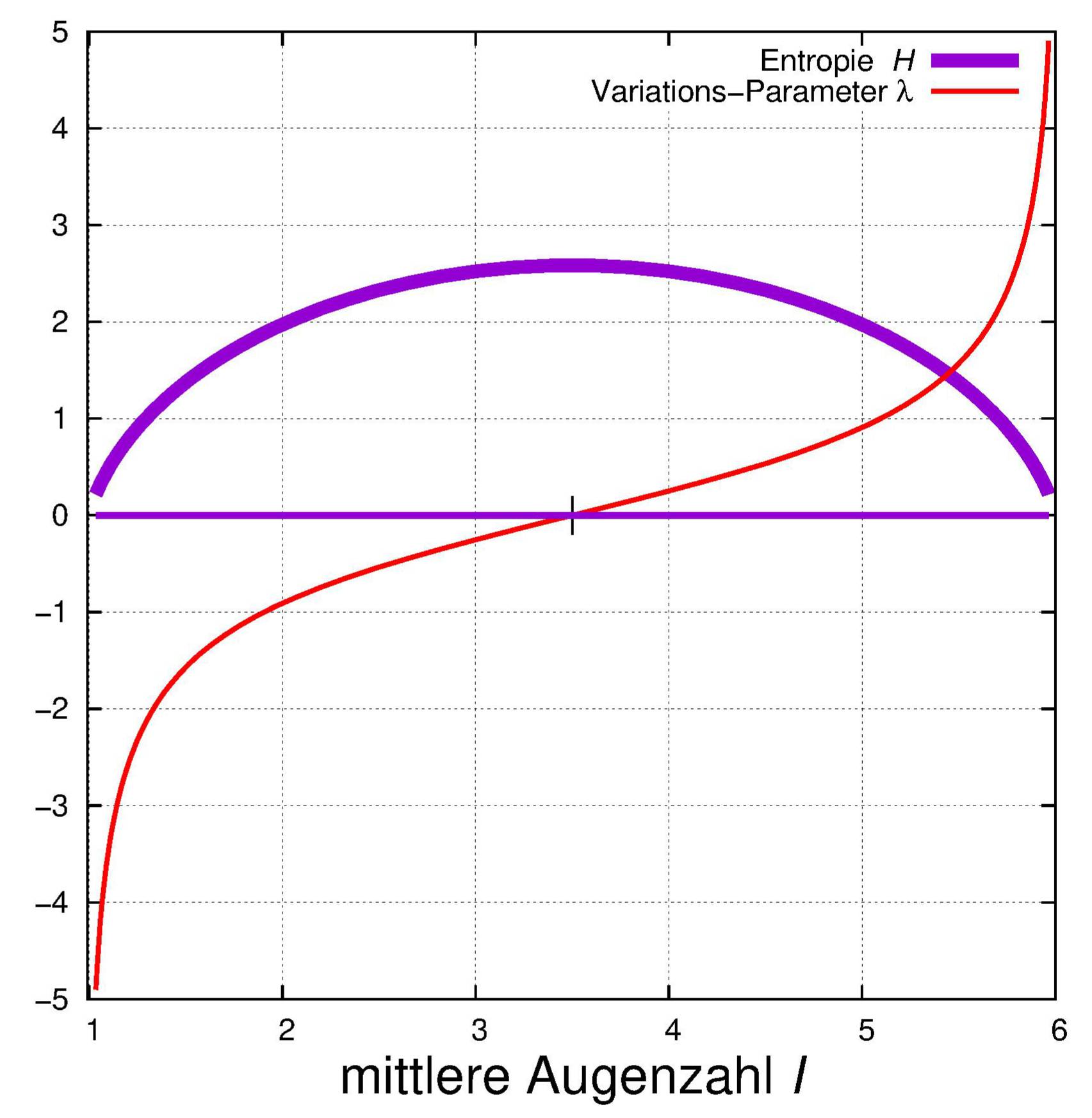
Die Nebenbedingung zur Bestimmung von λ₁ führt auf eine nicht geschlossen lösbare algebraische Gleichung fünften Grades für 2^λ₁(I). Ihre Umkehrung ist jedoch eine lineare Gleichung für I(λ₁). Hiermit lassen sich die maximale Entropie und der Lagrange-Multiplikator λ₁ als Funktionen der mittleren Augenzahl I wie in der folgenden Abbildung darstellen.

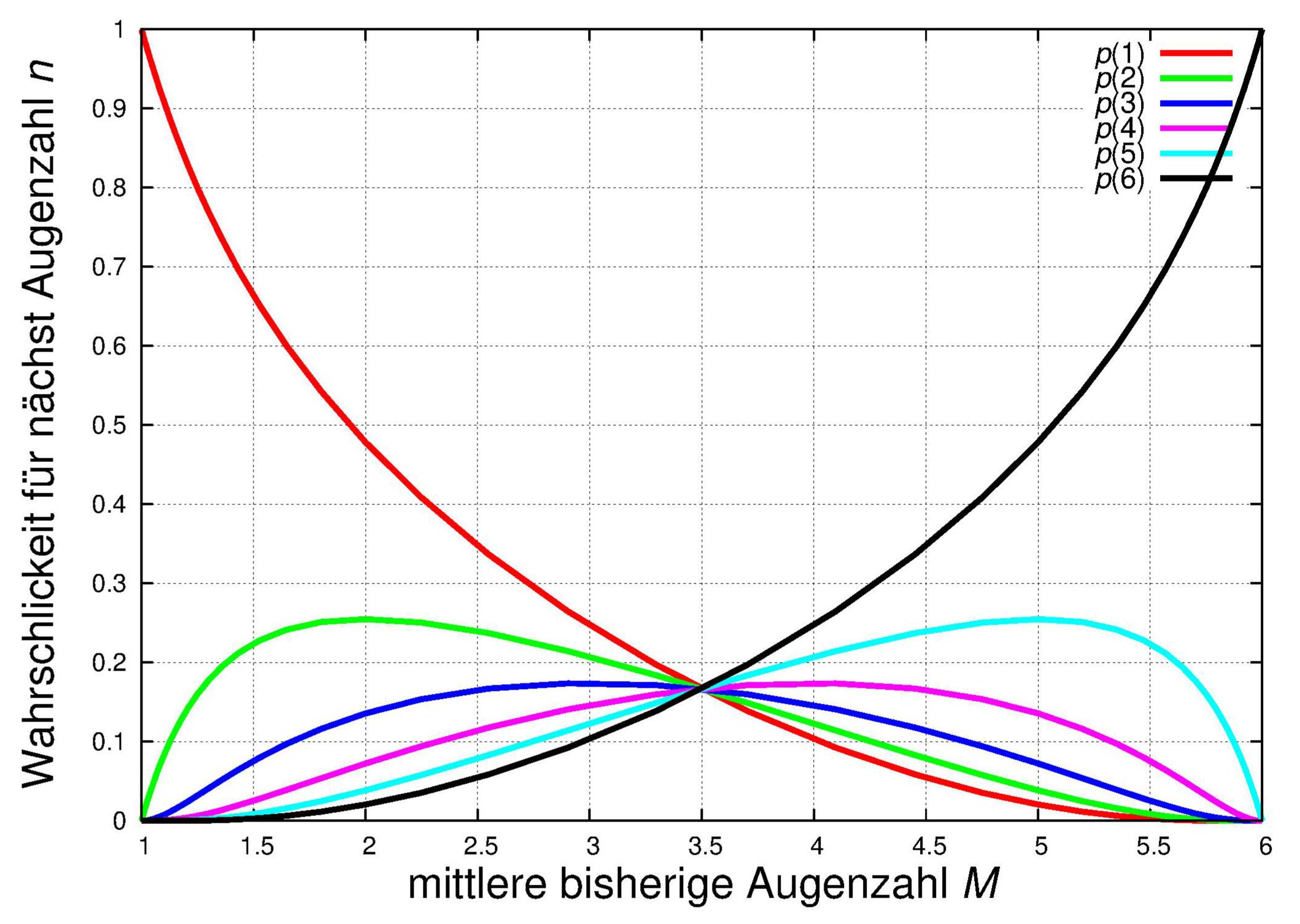
Für I = 3.5 ist λ₁ Null. Das entspricht dem idealen Würfel, und alle p_i, die in der Abbildung als Funktion der mittleren Augenzahl gezeichnet sind, sind dann gleich 1/6. Die maximale Entropie ist – wie im Abschnitt über Entropie schon allgemein bewiesen worden war und wie die Abbildung zeigt – kleiner oder gleich ld 6 ≅ 2.585 wie beim idealen Würfel. Die Vorhersagbarkeit vergrößert sich bei einem unsymmetrischen Würfel.

Bei mittleren Augenzahlen von 1 oder 6 ist die Entropie Null und der nächste Wurf vorhersagbar. Die Wahrscheinlichkeit p_i(I) hat ihr Maximum bei I = i.

Man sieht aber auch, wenn die mittlere Augenzahl unter 3.5 lag, daß p₁ > p₂ > p₃ > p₄ > p₅ > p₆ für die Wahrscheinlichkeiten gilt. Man müßte dann immer eine Eins vorsagen. Wenn sie über 3.5 lag, ist es genau umgekehrt, und die beste Vorhersage wäre jetzt immer die Sechs.

Je besser einer von mehreren Spielern die bisherige mittlere Augenzahl kennt, um so mehr könnte er dies also u. U. unfair nutzen. Der Nutzen dieser Kenntnis ist zwar gering. Wegen der ebenfalls geringen Vorinformation, nämlich nur über die bisherige mittlere Augenzahl, ist das auch nicht überraschend.

Eine kontinuierliche Verteilung:

Wir wählen dasselbe Beispiel wie schon vorher, bei dem die mittlere Signalenergie vorgegeben ist. Anders als vorher geben wir jetzt nicht die Form der Verteilung vor und zeigen, daß sie die Entropie maximalisiert, sondern bestimmen die Verteilung aus der Forderung nach maximaler Entropie. Zu erfüllen seien die Bedingungen

Auch hier verwenden wir die Variationsrechnung und definieren ein Funktional

das wir nach einem Parameter α variieren:

Für das Verschwinden der Variation ist hinreichend und wegen der beliebig wählbaren α-Abhängigkeit auch notwendig, daß die Klammer gleich Null ist. Hieraus ergibt sich als erstes

Aus der Normierung der Verteilung p(x) ergibt sich sodann

Aus der Mittelwertbedingung folgt λ₁ = 0 und somit

Für reellwertige Verteilungen muß λ₂ negativ sein. Die Bedingung, in der die mittlere Energie vorgegeben wird, liefert

Notwendig für maximale Entropie ist danach also λ₂ = −1/(2σ²) und schließlich die zu erwartende Gaußverteilung