Quellenkodierung

Die durch ungleich wahrscheinlich auftretende Zeichen einer Nachrichtenquelle bedingte Redundanz läßt sich verringern oder beseitigen, indem man diese Zeichen durch andere Zeichen darstellt (kodiert), deren Wahrscheinlichkeiten einer Gleichverteilung näherkommen oder sie erreichen. Hierfür gibt es einige Verfahren, von denen hier zwei diskutiert werden sollen.

Fano- und Huffman-Kodierung

Wir betrachten als einfachstes Beispiel einen Zeichenvorrat X aus vier zweistelligen Binärzeichen x_i, die in der folgenden Tabelle nach fallenden Wahrscheinlichkeiten p_i angeordnet sind.

Die ursprüngliche Entropie dieses Zeichensatzes ist

während sein Entscheidungsgehalt

ist. Die Redundanz beträgt daher

Diesen Zeichen ordnen wir nun im Sinne der Fano-Kodierung neue Zeichen y_i folgendermaßen zu: Wir teilen von oben beginnend die alten Zeichen in zwei gleichwahrscheinliche Hälften ein. Dies ist durch die waagerechte Trennlinie markiert. Die Zeichen in der oberen Hälfte erhalten eine 0, die in der unteren eine 1. Solange eine Hälfte noch mehr als ein Zeichen enthält, teilen wir sie wieder auf und ordnen ihren Zeichen auf die gleiche Art ein weiteres binäres Ausgangszeichen zu. Wir sehen an dem Beispiel, daß die Ausgangszeichen ungleich lang werden. Den wahrscheinlicheren Eingangszeichen werden dabei die kürzeren Ausgangszeichen zugeteilt, so daß im Mittel pro Zwei-Bit-Eingangszeichen nur 7/4 Binärzeichen entstehen, und zwar je 7/8 Nullen und 7/8 Einsen. In dieser Gleichverteilung drückt sich aus, daß die Redundanz der Quelle beseitigt worden ist.

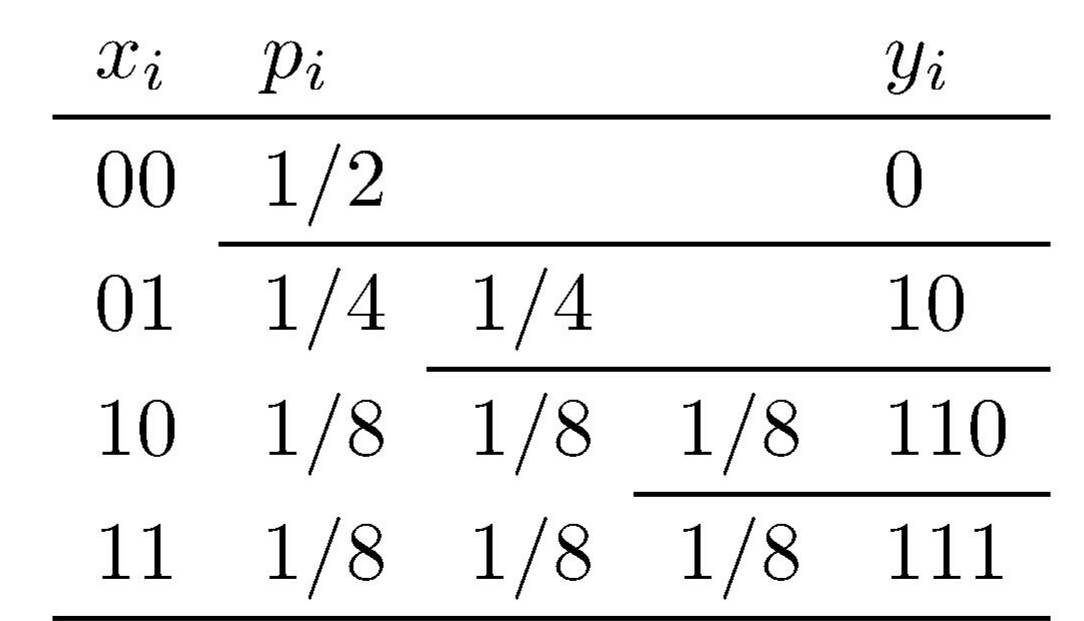
Der Fano-Kode ist ein Präfix-Kode. Das bedeutet: Kein Kodewort ist Präfix (Anfang) eines anderen Kodewortes. Dadurch ist der Kode sofort, d. h. ohne daß nachfolgende Zeichen abgewartet werden müssen, dekodierbar.

Eine Alternative zur Fano-Kodierung ist die Kodierung nach Huffman (siehe etwa Grams. p. 38), ebenfalls ein Präfix-Kode. Auch hier ordnet man die Zeichen nach fallender Wahrscheinlichkeit, beginnt aber mit der Kodierung bei den seltensten Zeichen. Als erstes erhält das seltenste Zeichen eine 0 und das zweitseltenste eine 1 an der letzten Stelle. Diese beiden Zeichen werden nun zusammengefaßt, so daß ihre Kombination die Summe ihrer Wahrscheinlichkeiten bekommt. Mit den übrigen Zeichen und diesem Kombinationszeichen wird nun wie vorher verfahren. Bei diesem auch hierfür besonders günstigen Beispiel ergeben sich die gleichen Kodewörter und damit die gleiche vollständige Redundanzbeseitigung wie bei der Fano-Kodierung.

Im allgemeinen aber sind die Wahrscheinlichkeiten der zu kodierenden Zeichen nicht so verteilt, daß sich durch alle Kodierungsschritte hindurch zwei gleichgroße Teile ergeben.

Anwendung auf eine reale Nachrichtenquelle

Als Beispiel betrachten wir die relativen Häufigkeiten, mit denen in einer gewissen Textprobe die großen Buchstaben des Alphabets vorkommen. Die folgende Tabelle zeigt, was das Fano-Kodierungsverfahren und die nächste Tabelle, was das Huffman-Kodierungsverfahren in diesem Fall leistet.

Zeichen	Wahrscheinlichkeit	Kodewort	Wortlänge
C	0.161068	00	2
E	0.110578	010	3
D	0.080325	0110	4
T	0.069476	01110	5
A	0.067390	01111	5
S	0.067390	100	3
I	0.060088	1010	4
V	0.046943	10110	5
R	0.046109	10111	5
N	0.044857	1100	4
M	0.043814	11010	5
O	0.041310	11011	5
L	0.039015	11100	5
X	0.025454	11101	5
P	0.017317	111100	6
U	0.015022	1111010	7
Y	0.014187	1111011	7
F	0.013979	111110	6
B	0.013353	1111110	7
G	0.006885	11111110	8
H	0.005633	111111110	9
W	0.004799	1111111110	10
K	0.002921	11111111110	11
Q	0.001460	111111111110	12
J	0.000417	1111111111110	13
Z	0.000209	11111111111110	14

Fano-Kodierung

Zeichen	Wahrscheinlichkeit	Kodewort	Wortlänge
C	0.161068	001	3
E	0.110578	101	3
D	0.080325	0001	4
T	0.069476	0100	4
A	0.067390	0111	4
S	0.067390	0110	4
I	0.060088	1000	4
V	0.046943	1100	4
R	0.046109	1101	4
N	0.044857	1110	4
M	0.043814	1111	4
O	0.041310	00000	5
L	0.039015	01010	5
X	0.025454	10011	5
P	0.017317	000011	6
U	0.015022	010110	6
Y	0.014187	010111	6
F	0.013979	100100	6
B	0.013353	100101	6
G	0.006885	00001000	8
H	0.005633	00001001	8
W	0.004799	00001011	8
K	0.002921	000010100	9
Q	0.001460	0000101010	10
J	0.000417	00001010110	11
Z	0.000209	00001010111	11

Huffmann-Kodierung

Die Kodierungen liefern unterschiedliche Ergebnisse:

Die Wortlänge bleibt bei Huffman mit fallender Zeichenwahrscheinlichkeit entweder gleich oder nimmt zu, während sie bei Fano an gewissen Stellen auch sprungweise wieder abnimmt.
Bei der Fano-Kodierung variiert die Wortlänge zwischen 2 und 14 und beträgt im Mittel 4.1922 Zeichen, während sie sich bei der Huffman-Kodierung von 3 bis 11 Binärzeichen erstreckt mit dem Mittelwert 4.099 Zeichen.
Die Huffman-Kodierung hat die Eigenschaft, daß es unter allen eindeutig dekodierbaren Kodierungen keine mit kürzerer mittlerer Wortlänge gibt.
Entscheidend: Während sich in diesem Beispiel bei der Fano-Kodierung die Redundanz von 4.7004 auf 4.1922, also um 10.81% verringert, schafft die Huffman-Kodierung eine Reduktion um 13.22% auf 4.078.

Quellenkodierung im allgemeineren Fall

Die Fano-Kodierung wie auch die Kodierung nach Huffman beseitigt die Redundanz einer Zeichenquelle nur dann völlig, wenn sich die Zeichen einer Quelle bis zur eindeutigen Identifizierung immer in gleichwahrscheinliche Hälften einteilen lassen. Wenn dies nicht gegeben ist, bleibt Redundanz zurück.

Wie und wie gut läßt sich Redundanz nun beseitigen, wenn sich die Zeichen nicht immer in genau gleichwahrscheinliche Hälften gruppieren lassen?

Shannon (1948) hat gezeigt, daß man die Redundanz auch in diesem Fall durch geeignete Kodierung beliebig reduzieren kann. Sein entscheidender Gedanke war, nicht die Zeichen der Quelle einzeln zu kodieren, sondern ausreichend viele von ihnen zu neuen Wörtern der Länge N zusammenzufassen und diese zu kodieren. Wenn die Quelle n voneinander unabhängige Zeichen x_i mit den Wahrscheinlichkeiten p_i und somit die Entropie 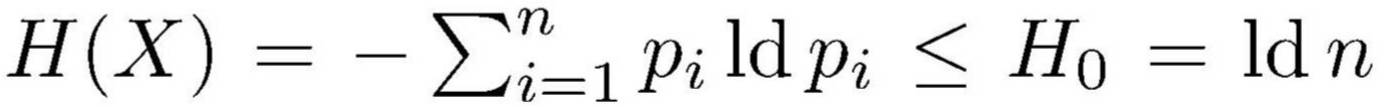hat, dann ist die Wahrscheinlichkeit p eines jeden solchen zusammengesetzten Wortes einheitlich näherungsweise

Die Gesamtwahrscheinlichkeit dieser Wörter kann durch eine genügend große Wortlänge N beliebig nahe an Eins gebracht werden (Shannon, Anh. 3). Daher muß die Anzahl dieser annähernd gleichwahrscheinlichen Wörter ungefähr gleich 2^NH(X) sein.

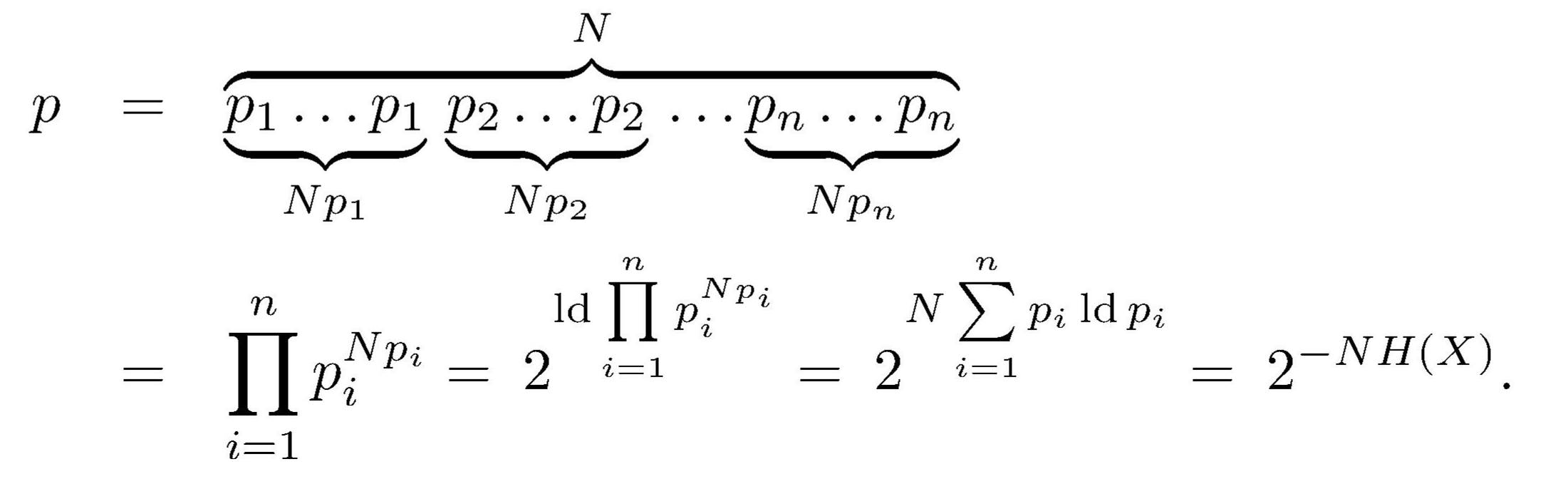
Man braucht somit NH(X) bit, um anzugeben, welches von ihnen vorliegt. Jedes der N Zeichen eines derart kodierten Wortes läßt sich auf diese Art also durch H(X) ≤ H₀(X) = ld n bit und somit redundanzfrei darstellen.

Diese 2^NH(X annähernd gleichwahrscheinlichen Wörter sind allerdings nur ein kleiner Bruchteil aller n^N Wörter der Länge N. Das Verhältnis ist

So ist z. B. bei Binärzeichen (n = 2), wenn sie mit den Wahrscheinlichkeiten 3/4 und 1/4 entsprechend einer Entropie von H(X) ≈ 0.8113 auftreten und zur Kodierung zu Wörtern der Länge N = 400 (siehe unten) zusammengefaßt werden, dieses Verhältnis ungefähr gleich 2^{400(1 - 0.8113)} ≈ 2⁷⁵ oder 10²³.

Die übrigen viel zahlreicheren fast n^N Wörter lassen sich unter Verzicht auf Einsparungen je mit ld(n^N) = N ld n = NH₀(X) ≥ NH(X) bit kodieren. Da aber ihre Gesamtwahrscheinlichkeit durch ausreichende Wortlänge N beliebig klein gemacht werden kann, tragen sie vernachlässigbar wenig zum mittleren Zeichenbedarf bei. Wir können dieses Ergebnis als Fundamentalsatz der Quellenkodierung (Shannon, 1948) formulieren:

Faßt man eine zu kodierende Nachricht in genügend langen Zeichenfolgen zusammen, dann lassen sich diese so kodieren, daß die Redundanz beliebig klein wird.

Die hierdurch eingeführten neuen Zeichen müssen allerdings ziemlich lang sein, damit ihre Gleichwahrscheinlichkeit ausreichend gewährleistet ist. Das Quellzeichen x_i kommt in jedem neuen Zeichen der Länge N. im Mittel N p_i mal vor. Soll diese Häufigkeit um nicht mehr als 10 % schwanken, dann muß gelten

und daher

In dem eben genannten binären Beispiel war p_i ≥ 1/4. Die neuen Zeichen müssen also aus mindestens 400 Quellzeichen bestehen. Jedes von ihnen ist durch NH(X) = 400 • 0.8113 bit ≈ 325 bit zu kodieren, da es von ihnen 2³²⁵ ≈ 10⁹⁸ verschiedene gibt. Die Übertragung würde sich dadurch um 400 Zeichen verzögern. Das Verfahren setzt im übrigen offensichtlich voraus, daß die Originalnachricht genügend lang ist.

Die Bedeutung dieses Verfahrens liegt also weniger in seiner technischen Anwendbarkeit als darin, daß es zeigt, daß Redundanz wegen ungleich wahrscheinlicher Zeichen theoretisch beliebig gut beseitigt werden kann.