Markoff-Prozesse

Der klassische Markoff-Prozeß ist die natürliche Sprache. Sie hat neben ihrer Redundanz durch ungleich häufige Zeichen eine beträchtliche Vorhersagbarkeit jedes Zeichens durch seine Vorgänger (beides gilt für Schrift- wie für Lautzeichen). Shannon hat dies an der englischen Schriftsprache veranschaulicht. Je weiter man die Einwirkung vorausgehender Buchstaben einer Zufallsfolge von Zeichen statistisch an diejenige der wirklichen Sprache angleicht, um so mehr nähert sich ihr ein solcher sinnloser Text. Hier seine Beispiele unter Verwendung von 26 Großbuchstaben und dem Zwischenraum:

Näherung nullter Ordnung (Zeichen voneinander unabhängig und gleich wahrscheinlich)
XFOML RXKHRJFFJUJ ZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZLHJQD.
Näherung erster Ordnung (Zeichen voneinander unabhängig, jedoch mit Häufigkeiten des englischen Textes
OCRO HLI RGWR NMIELWIS EU LL NBNESEBYA TH EEI ALHENHTTPA OOBTTVA NAH BRL.
Näherung zweiter Ordnung (Digramm-Struktur wie im Englischen)
ON IE ANTSOUTINYS ARE T INCTORE ST BE S DEAMY ACHIN D ILONASIVE TOCOOWE AT TEASONARE FUSO TIZIN ANDY TOBE SEACE CTISBE.
Näherung dritter Ordnung (Trigramm-Strukur wie im Englischen)
IN NO IST LAT WHEY CRATICT FROURE BIRS GROCID PONDENOME OF DEMONSTURES OF THE REPTAGIN IS REGOACTIONA OF CRE.
Näherung erster Ordnung, auf Wörter bezogen
REPRESENTING AND SPEEDILY IS AN GOOD APT OR COME CAN DIFFERENT NATURAL HERE HE THE A IN CAME THE TO OF TO EXPERT GRAY COME TO FURNISHES THE LINE MESSAGE HAD TO BE THESE.
Wortnäherung zweiter Ordnung
THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED.

Derartige Prozesse sollen nun formal behandelt werden.

Definitionen

Ein Markoff-Prozeß kann definiert werden durch

einen Zeichenvorrat X: = {x, . . . ,x_K}, aus dem er eine unendliche Folge von Zeichen schrittweise auswählt,
mögliche Zustände S_i (i = 1, . . . , n), die er (wiederholt) einnimmt,
je eine Wahrscheinlichkeitsverteilung p_ik für das Auftreten des nächsten Zeichens x_k im Zustand S_i,
Wahrscheinlichkeiten p(S_j|S_i) für den Übergang vom Zustand S_i in den Zustand S_j.

Eine Markoff-Quelle erzeugt bei jedem Übergang ein Zeichen. Die Folge dieser Zeichen heißt Markoff-Kette. Hier soll speziell der Fall betrachtet werden, daß die Zustände durch die vorangehenden Zeichen bestimmt sind. In diesem Fall ergeben sich die Übergangswahrscheinlichkeiten aus den Zeichenwahrscheinlichkeiten S_ik. Bei einem Alphabet mit K Zeichen und dem Einfluß von je r vorangehenden Zeichen gibt es n = K^r verschiedene Zustände S_i.

Stochastische Matrizen

Zur Beschreibung von Markoff-Prozessen ist ein Typ von Matrizen nützlich, die als stochastische Matrizen bezeichnet werden. Sie sind definiert durch die beiden Eigenschaften

Ihre Elemente sind nichtnegativ.
Alle Zeilensummen sind gleich Eins.

Daraus folgen recht einfach die folgenden drei Sätze.

Wenn A und B stochastische Matrizen sind, dann ist auch die Produktmatrix C = A B stochastisch.

Beweis:

Das Matrixelement

ist als Summe von Produkten nichtnegativer Zahlen selber nichtnegativ.
Die Zeilensummen von C sind

Beides gilt auch für nichtquadratische Matrizen, wenn nur die Spaltenzahl von A gleich der Zeilenzahl von B ist.

Jede quadratische stochastische Matrix A hat den Eigenwert 1, d. h. es gibt einen Zeilenvektor x mit A = x.

Beweis:

Hinreichend hierfür ist, daß die Determinante det(A − E) gleich Null ist (E = Einheitsmatrix). Weil in A alle Zeilensummen gleich Eins sind, sind in A − E alle Zeilensummen gleich Null. Wir ersetzen in der Determinante irgendeine Spalte durch die Summe aller Spalten und erhalten dort lauter Nullen. Also ist det(A − E) = 0.

Mit der quadratischen stochastischen Matrix A hat auch Aⁿ den Eigenvektor x zum Eigenwert 1.

Beweis durch vollständige Induktion nach n:

Für n = 1 gilt der Satz nach Voraussetzung. Wenn er für n − 1 gilt, dann folgt er auch für n, da

ist. Mit x ist auch jedes Vielfache davon ein Eigenvektor. Hier sind insbesondere diejenigen Eigenvektoren von Bedeutung, deren Komponenten Wahrscheinlichkeiten sind und daher so normiert sind, daß sie die Summe Eins haben. Wenn die stochastische r*r-Matrix (A − E) den Rang (r − s) hat, sind die Eigenvektoren Lösungen des homogenen Gleichungssystems x (A − E) = 0 mit s freien Parametern. Im Falle s = 1 ist ein normierter Eigenvektor also eindeutig bestimmt.

Beispiel: Eine Markoff-Quelle der Rückwirkung 2

Gegeben seien (siehe Heise und Quattrocchi, 1983)

ein binärer Zeichensatz
die durch die vorangehenden beiden Zeichen bestimmten vier Zustände
Im Zustand S_i sei das Zeichen x_k mit der Wahrscheinlichkeit p_ik zu erwarten. Diese Wahrscheinlichkeiten sind in der folgenden Matrix P zusammengefaßt:
Anfänglich mögen die vier Zustände mit den Wahrscheinlichkeiten

vorliegen.

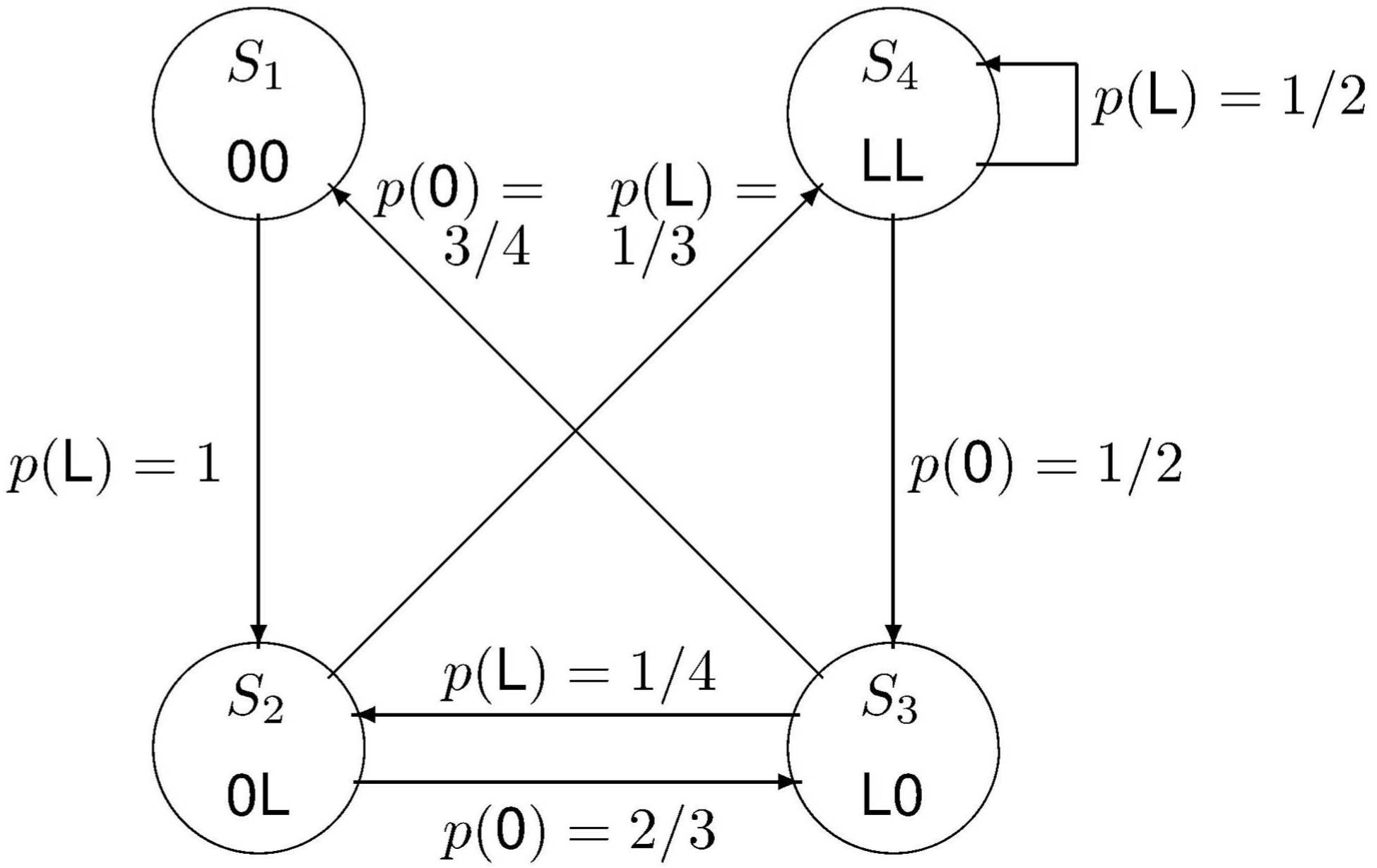
Zustandsgraph für eine Markoff-Quelle der Rückwirkung r = 2 (nach Hamming, 1980)

Diese Markoff-Quelle kann durch diesen Zustandsgraphen dargestellt werden.

Hierin geht der Zustand S_j aus dem Zustand S_i mit der Wahrscheinlichkeit p(S_j|S_i) hervor. Diese Übergangswahrscheinlichkeiten ergeben sich hier aus der Definition der Zustände und aus den Zeichenwahrscheinlichkeiten. Sie lassen sich zu einer quadratischen stochastischen Matrix, der Markoff-Matrix zusammenfassen:

Bei einem binären Zeichensatz hat diese Matrix in jeder Zeile ein oder zwei von Null verschiedene Elemente. Diese sind identisch mit den Elementen in der gleichen Zeile der oben angegebenen Matrix P.

Aus dem Zeilenvektor π₀ der Anfangswahrscheinlichkeit der vier Zustände S_i wird nach Wahl des ersten Zeichens die Zustandswahrscheinlichkeit

Nach der Ausgabe von n Zeichen ist sie

Möchte man wissen, mit welchen Wahrscheinlichkeiten dann die Zeichen x_k, hier also O und L, zu erwarten sind, dann muß man deren für die einzelnen Zustande S_i als bekannt angenommenen Wahrscheinlichkeiten über alle (hier also vier) Zustände mitteln. Dies ergibt – als Vektor p_(n) geschrieben –

Die Beispiel-Markoff-Matrix M hat den Eigenvektor

zum Eigenwert Eins. Man findet ihn als Lösung des linearen Gleichungssystems π (M − E) = 0, ergänzt durch die Bedingung, daß die Summe der Komponenten von π gleich Eins ist. Wie wir für stochastische Matrizen schon allgemein gesehen hatten, ist dieser Vektor dann auch Eigenvektor zu allen Potenzen der Matrix M. Haben die Zustände irgendwann im Laufe eines Markoff-Prozesses diese Wahrscheinlichkeiten, dann ändern sie sich also nie mehr.

Die Potenzen der Markoffschen Übergangsmatrix Mⁿ streben in diesem Beispiel mit wachsendem n gegen den Grenzwert

Man erkennt das, indem man nachrechnet, daß M • M^∞ = M^∞ ist, wobei man verwendet, daß die Zeilensummen von M gleich Eins sind. (Nicht jede stochastische Matrix hat allerdings eine Grenzmatrix M^∞.)

Unabhängig von der Wahl der anfänglichen Zustandsverteilung~$\Vec{\pi}_0$ strebt, wie eine gleiche Rechnung zeigt, die Folge~$\Vec{\pi}_0, \Vec{\pi}_1,\ldots$ gegen den Eigenvektor

Bei Beginn einer Beobachtung eines Markoff-Prozesses ist möglicherweise offen, in welchem Zustand er sich befindet. Wenn man von vorn herein die sich im Laufe des Markoff-Prozesses einstellende stationäre Zustandsverteilung π, also den Eigenvektor der Markoff-Matrix, annimmt, verzichtet man darauf, einen eventuell ablaufenden `Einschwing'-vorgang für die Wahrscheinlichkeitsverteilung der Zustände zu berücksichtigen.

Selbst wenn man den Anfangszustand eines Markoff-Prozesses mit Sicherheit kennt, läßt sich sein Verlauf nur im Sinne von Wahrscheinlichkeiten vorhersagen. Dies gilt ja bereits für die Zustandsverteilung nach dem ersten Schritt. Auch in dieser Situation ist für Vorhersagen über mehrere Schritte hinweg die stationäre Verteilung π₀ eine sinnvolle Näherung. An einem vertrauten Beispiel illustriert: Bei geschriebenem Text kann man zwar noch die nächsten ein, zwei oder drei Buchstaben aufgrund ihres Zusammenhanges mit den vorangehenden Zeichen abweichend von ihrer mittleren Häufigkeit im Text recht gut vorhersagen, für etwa den zwanzigsten bleibt einem jedoch nicht viel mehr Information übrig als die mittlere Häufigkeit

p = π_∞ P.

Im betrachteten Beispiel ist der Vektor p gleich (21, 20)/41.

Die einfachste Approximation einer rückwirkungsbehafteten Markoff-Quelle ist daher die durch eine rückwirkungsfreie Quelle, deren Zeichen diese über alle Zustände gemittelten Wahrscheinlichkeiten p haben.

Eine Markoff-Matrix M heißt regulär, wenn eine Grenzmatrix M^∞ existiert, deren Zeilen alle gleich dem Eigenvektor der Grenzzustandsverteilung π_∞ sind. Nicht alle Markoff-Matrizen haben diese Eigenschaft, wie das folgende Gegenbeispiel zeigt:

Trotzdem gibt es hier als Eigenvektoren aller Potenzen von M die eindeutige stationäre Zustandverteilung π = (1/2, 1/2).

Klassifikation von Markoff-Prozessen

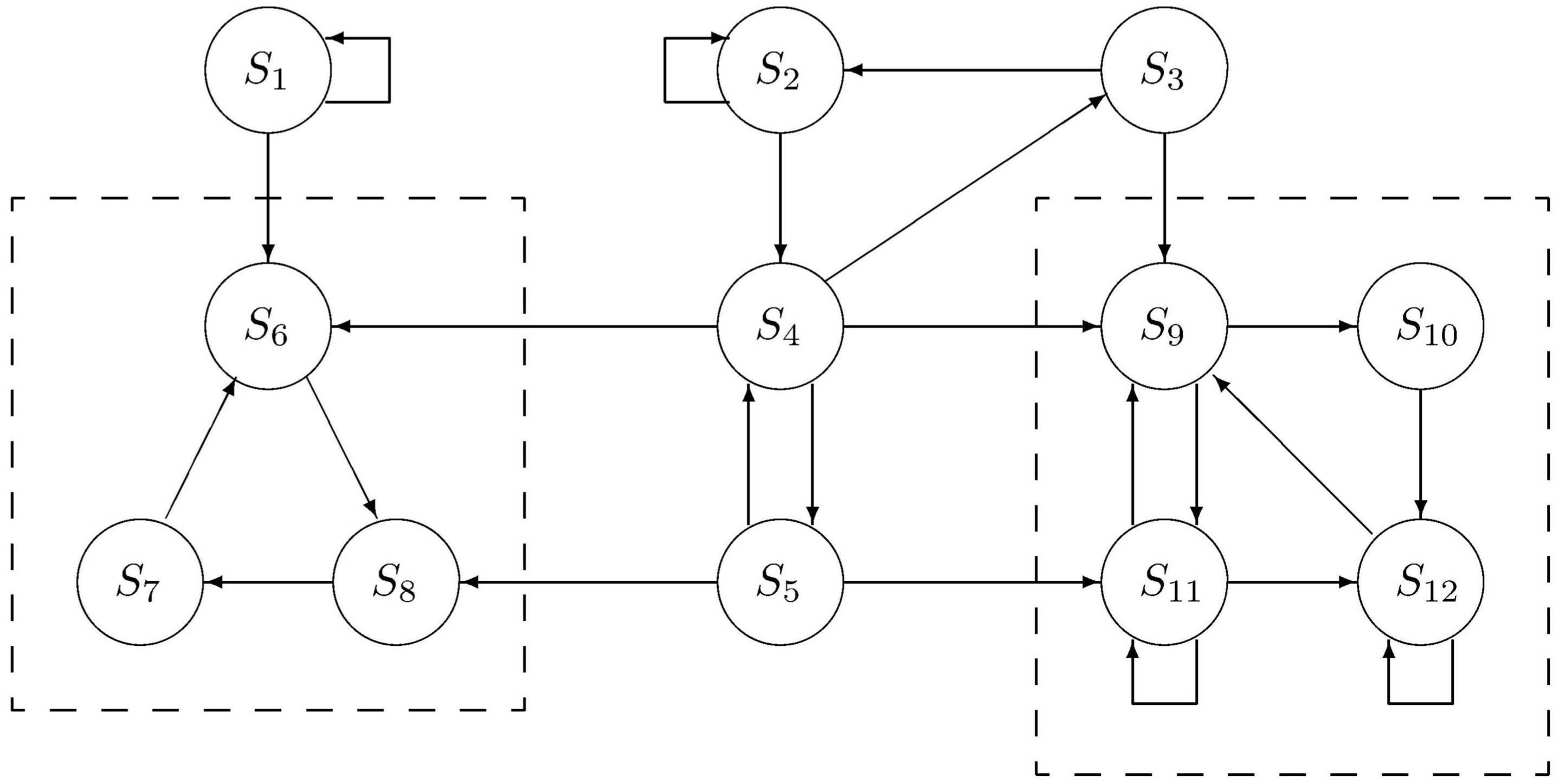
Die Menge der Zustände eines Markoff-Prozesses kann in Teilmengen unterschiedlichen Charakters zerfallen, und zwar in

Teilmengen vergänglicher Zustände, Teilmengen,
Teilmengen wesentlicher Zustände, die alle wiederholt durchlaufen werden können, nachdem einer von ihnen einmal erreicht worden ist, und keinen Zugang zu einer anderen solchen Teilmenge bieten.

Dies ist in der folgenden Abbildung am Beispiel dargestellt. Teilmengen vergänglicher Zustände sind {S₁} und {S₂, . . . , S₅}. Teilmengen von wesentlichen Zuständen sind {S₆, . . . , S₈} und {S₉, . . . , S₁₂}. Im einfachsten Fall bestehen die Zustände nur aus einer einzigen Menge wesentlicher Zustände. Solche Markoff-Prozesse werden als ergodisch bezeichnet (Hamming, 1980).

Vorhersage-Kodierung

Wie kann man im Sinne einer Quellenkodierung die Redundanz einer Markoff-Quelle durch Kodierung verringern, so daß also die Vorhersagbarkeit ihrer Zeichen geringer wird?

Hierzu läßt sich ein ganz allgemeines Prinzip anwenden, das der Vorhersage-Kodierung (engl. predictive encoding, siehe z. B. Hamming, p. 88). Es besteht darin, daß auf der Senderseite ein Prädiktor (etwa ein dafür programmierter Rechner) das kommende Zeichen vorhersagt und der Sender statt des Zeichens seine Abweichung von der Vorhersage überträgt. Der Empfänger stellt mit einem identischen Prädiktor aus den Abweichungen wieder das Originalsignal her.

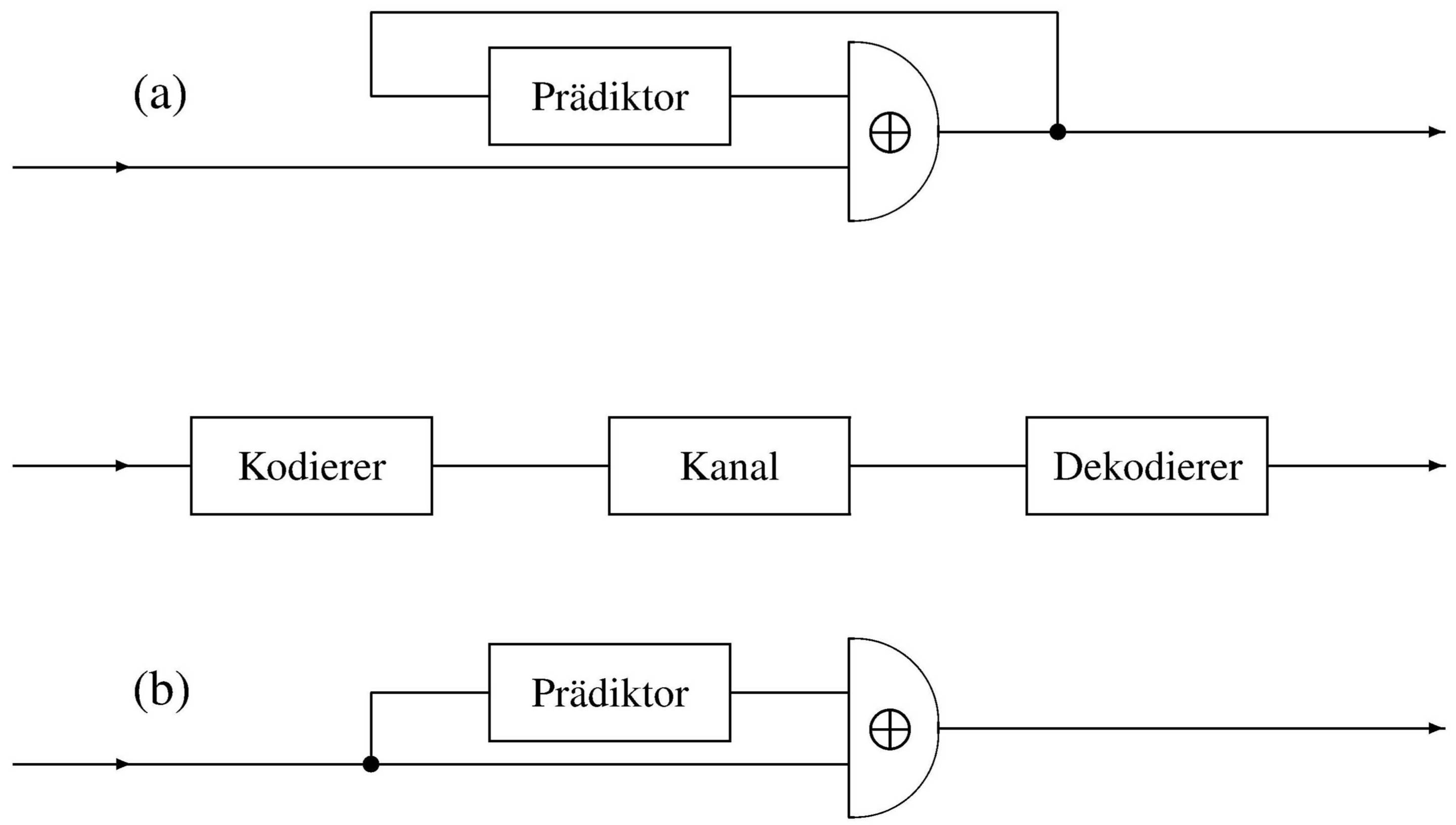
Prinzip der Vorhersage-Kodierung (nach Hamming, 1980)
(a) Vorhersage-Kodierung und (b) -Dekodierung

Im günstigsten Fall kann alle Vorhersagbarkeit, d. h. alle Redundanz aus der tatsächlich übertragenen Nachricht entfernt werden. Das setzt voraus, daß der Kodierer möglichst alle Information ausnutzt, die er über die Quelle hat oder im Betrieb gewinnt, also die Kenntnis der mittleren Zeichenhäufigkeiten, insbesondere aber auch des aktuellen Zustandes der Quelle aufgrund der vorangehenden Zeichen.

Wie die Einsparung an Redundanz praktisch genutzt werden kann, sei am Beispiel einer binären Quelle in der Abbildung gezeigt. Sie liefert eine Folge von Nullen und Einsen, die in einem XOR-Gatter verglichen werden mit einer Folge, die von der Vorhersageeinrichtung geliefert wird. Im ungünstigsten Fall, wenn zur Vorhersage keine Kenntnis über die Quelle herangezogen wird, sind Nullen und Einsen am Gatterausgang gleichwahrscheinlich. Je perfekter die Vorhersage aber ist, um so mehr Nullen gibt das Gatter ab. Dies läßt sich nutzen durch eine Kodierung, bei der anstelle der Binärzeichen die Länge der Nullenfolgen übertragen wird.

Auf der Empfängerseite wird zunächst diese Lauflängenkodierung rückgängig gemacht. Die entstehende Binärfolge wird in eine identische Vorhersageeinrichtung eingespeist, deren Ausgang wiederum in einem XOR-Gatter mit der gesendeten Folge verglichen wird. Dessen Ausgang ist das Originalsignal.