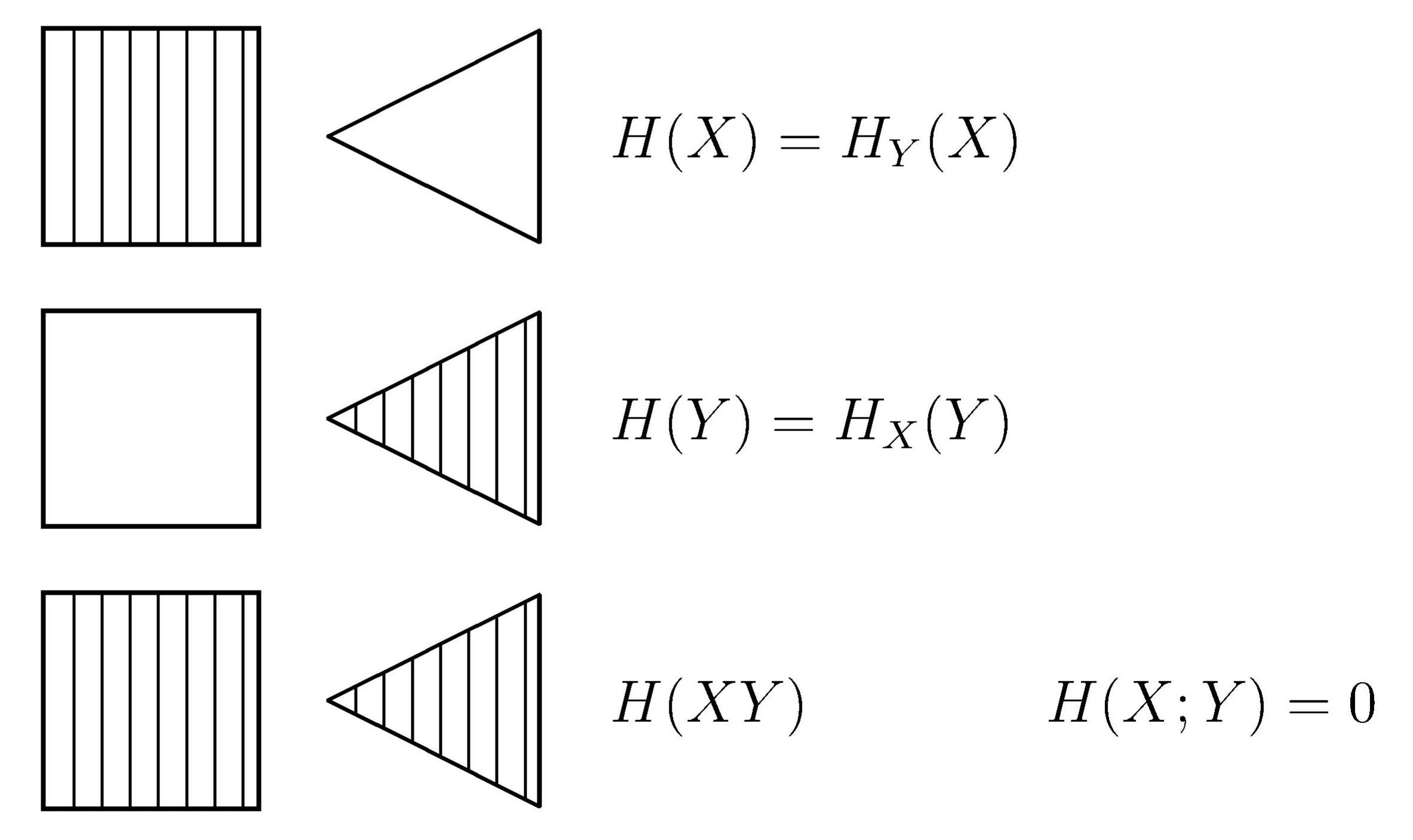Informationsübertragung
Die Übertragung von Information über Nachrichtenkanäle (von hier nach da)
oder Nachrichtenspeicher (von jetzt nach dann)
kann man sich aus zwei Ereignissen zusammengesetzt vorstellen,
-
der Auswahl von Zeichen xi
aus einem senderseitigen Zeichenvorrat X,
-
der zugehörigen Auswahl von Zeichen yk aus einem empfängerseitigen
Zeichenvorrat Y.
Im Idealfall sind beide Zeichenvorräte gleich, und die Zuordnung der beiden Zeichen ist umkehrbar eindeutig.
Unter realen Bedingungen kann diese Eindeutigkeit gestört sein.
Störungen sind – wie auch die Nutzinformation – teilweise oder gänzlich
unvorhersagbar und lassen Unvorhersagbarkeit in die Folge der
empfängerseitigen Zeichen einfließen.
Der Begriff Entropie ist daher ein geeignetes Mittel, die Möglichkeiten der
Informationsübertragung über einen realen Nachrichtenkanal zu beschreiben.
Entropien sind durch Wahrscheinlichkeiten auszudrücken, hier insbesondere
durch Wahrscheinlichkeiten von
Verbundereignissen xiyk, die aus den
senderseitigen Ereignissen xi und den empfängerseitigen
Ereignissen yk zusammengesetzt sind.
Die Wahrscheinlichkeit p(xiyk)
eines solchen Verbundereignisses hängt mit den Wahrscheinlichkeiten p(xi)
und p(yk) der beiden Einzelereignisse durch
zusammen.
Die Faktoren der Form pa(b) –
häufig auch p(b|a) geschrieben – sind
die Wahrscheinlichkeiten für das Auftreten des Ereignisses bunter der
Bedingung, daß auch das Ereignis a eingetreten ist.
Sind beide Ereignisse unabhängig voneinander, dann gibt es keine solche Bedingung.
Die Verbundwahrscheinlichkeit ist dann das Produkt der unbedingten
Einzelwahrscheinlichkeiten:
Bei unvereinbaren Ereignissen sind die bedingten Wahrscheinlichkeiten
pxi(yk) und
pyk(xi) und damit auch die
Verbundwahrscheinlichkeit p(xiyk) gleich Null.
Unvereinbare Ereignisse sind natürlich nicht unabhängig voneinander.
Die Wahrscheinlichkeiten für die Ereignisse xi
und yk können durch die
Verbundwahrscheinlichkeiten ausgedrückt werden.
Es gilt
Verwendet man auf den rechten Seiten die Beziehungen~(\ref{eq:8-1}),
so sieht man, daß auch die bedingten Wahrscheinlichkeiten normiert sind:
Aus~\eqref{eq:8-3} sowie~\eqref{eq:8-4} ergibt sich: auch die Verbundwahrscheinlichkeit ist auf Eins normiert:
Die Normierung gilt dann also auch für die Wahrscheinlichkeiten der Einzelereignisse.
Wir definieren zunächst die Verbund-Entropie
Wie sie lassen sich auch die Entropien der Einzelereignisse
durch die Verbundwahrscheinlichkeiten ausdrücken:
Satz:
Die Verbund-Entropie ist nie größer als die Summe der Entropien
der Teilereignisse:
H(XY) ≤ H(X) + H(Y).
Beweis unter Verwendung von
ln x ≤ x − 1 :
Der Übergang zur vorletzten Zeile zeigt, daß das Gleichheitszeichen im Satz genau dann gilt,
wenn
p(xiyk) = p(xi) p(yk) ist,
d. h. wenn alle Ereignisse aus X unabhängig von denen aus Y sind.
In den (interessanteren) anderen Fällen ist
H(XY) < H(X) + H(Y).
Im Fall unabhängiger Ereignisse läßt sich der Satz über die Verbundentroppie
durch vollständige Induktion auch auf Ereignisse verallgemeinern,
die aus mehr als zwei unabhängigen Komponenten zusammengesetzt sind.
Es gilt dann also die Gleichung
Wir können außerdem bedingte Entropien definieren.
So ist
die Empfängerentropie unter der Voraussetzung, daß das spezielle
Zeichen xi gesendet worden ist.
In diesem Maße bleibt (also insbesondere wegen Störungen) unbestimmt,
welches Zeichen yk der Empfänger
dem gesendeten Zeichen xi zuordnen soll.
Ebenso ist
die Senderentropie unter der Voraussetzung,
daß das spezielle Zeichen yk empfangen worden ist.
In diesem Maße bleibt (ebenso wegen Störungen) also unbestimmt, welches
Senderzeichen xi das empfangene Zeichen yk ausgelöst hat.
Durch Mittelung über alle Senderzeichen erhalten wir
als mittlere Empfängerentropie, nachdem irgendein Zeichen gesendet worden
ist.
Entsprechend ist
die mittlere Senderentropie, nachdem irgendein Zeichen empfangen worden ist.
Die bedingten Entropien HX(Y)
und HY(X) sind also geeignete Maße
für Störeinflüsse bei der Informationsübertragung.
Mit Hilfe der bedingten Entropien können wir an den als
Ungleichung formulierten Satz über Verbund-Entropien eine Gleichung anknüpfen:
Satz:
H(XY) = H(X) + HX(Y).
Beweis:
Ebenso gilt aus Symmetriegründen
Aus den Sätzen über die Verbund-Entropie folgt,
daß die bedingten Entropien kleiner oder gleich den unbedingten Entropien sind:
Das ist plausibel, denn jede Einflußnahme z. B. von X auf Y
verringert die Unsicherheit H(Y).
Bei perfekter Verbindung zwischen X und Y sind die bedingten Entropien gleich Null,
während das Gleichheitszeichen im völlig gestörten Fall gilt,
wo jeder Einfluß zwischen der Auswahl aus X und der Auswahl aus Y verlorengegangen ist.
Die hier für diskrete Ereignisse formulierten Aussagen gelten ebenso für den Fall,
daß Signale oder Meßwerte aus kontinuierlichen Bereichen ausgewählt werden.
Die Summationen sind dann durch Integrationen zu ersetzen.
Als Synentropie bezeichnet man den bezüglich X und Y symmetrischen Ausdruck
Die Ungleichung für die Verbundentropie sagt unmittelbar, daß
ist.
Das Gleichheitszeichen gilt darin genau dann, d. h. die Synentropie ist genau dann Null,
wenn X und Y unabhängig voneinander sind.
Zwei äquivalente, jedoch unsymmetrische Formen der Synentropie ergeben sich
aus den Gleichungen für die Verbund-Entropie:
Sie sind nützlich bei der Anwendung auf Nachrichtenübertragungskanäle, auf die noch eingegangen wird.
Synentropie wird dort meistens als mittlere Transinformation bezeichnet.
Wir erkennen an diesen unsymmetrischen Darstellungen,
daß die Synentropie H(X;Y) gleich H(X) wird,
wenn jedes Ereignis aus Y eindeutig festlegt,
welches Ereignis aus X stattgefunden hat (HY(X) = 0).
Ebenso wird H(X;Y) gleich H(Y),
wenn jedes Ereignis aus X eindeutig ein Ereignis
aus Y hervorruft (HX(Y) = 0).
Wir wollen uns zuerst ein Beispiel für zusammengesetzte
Ereignisse xiyk ansehen,
bei dem die Komponenten xi (i = 1, . . . ,6)
und yk (k = 1, . . . ,4) nicht unabhängig voneinander sind,
so daß die Wahrscheinlichkeit von Verbundereignissen auf
zu verallgemeinern ist.
Die Verbundwahrscheinlichkeiten seien in der folgenden Matrix vorgegeben.
Leere Felder bedeuten darin Wahrscheinlichkeit Null.
Der Index i läuft nach unten, der Index k nach rechts.
Die Zahlen am rechten und am unteren Rand sind die daraus durch spalten- bzw. zeilenweise Summation
resultierenden Wahrscheinlichkeiten
Die sich aus ergebenden bedingten Wahrscheinlichkeiten
sind in entsprechenden Matrizen dargestellt:
Die Zeilensummen von {pxi(yk)}
und die Spaltensummen von {pyk(xi)} sind, wie man sieht,
gleich Eins, während die Spaltensummen von {pxi(yk)} und die Zeilensummen von
{pyk(xi)} auch größer oder kleiner als Eins sein können.
Die Entropien (in bit) sind in diesem Beispiel
Wir finden zahlenmäßig die folgenden Sätze bestätigt:
Die Transinformation ist in diesem Beispiel
Wenn man die Entropien durch Flächen symbolisiert, lassen sich ihre
Beziehungen wie in der untenstehenden Abbildung geometrisch darstellen.
Um die Bedeutung der Abhängigkeiten zwischen den xi
und den yk zu illustrieren,
wollen wir die Teilwahrscheinlichkeiten p(xi) und
p(yk) mit denselben Zahlenwerten wie vorher verwenden,
jedoch zum Vergleich jetzt annehmen, daß Unabhängigkeit herrsche.
Dann resultieren daraus Verbundwahrscheinlichkeiten
p(xiyk)
= p(xi) p(yk),
die wir wie oben in eine Matrix eintragen:
Am rechten Rand stehen wieder die Wahrscheinlichkeiten p(xi),
am unteren Rand die p(yk).
Charakteristisch für die Unabhängigkeit ist, daß einerseits alle Zeilen
und andererseits alle Spalten einander proportional sind.
Die Entropien H(X) und H(Y) behalten
voraussetzungsgemäß natürlich
dieselben Werte wie im betrachteten abhängigen Fall.
Die Verbundentropie H(XY)
vergrößert sich jedoch,
da in der ursprünglichen Ungleichung für die Verbund-Entropie jetzt das Gleichheitszeichen gilt und
die Verbundwahrscheinlichkeiten gleichmäßiger über die Matrix verteilt sind.
Sie beträgt
Es bestätigt sich hier die Gleichung
und die mittlere Transinformation ist Null:
Eine wie auch immer geartete Wahl aus X gibt keinen Hinweis darauf,
welche Wahl aus Y zu treffen ist.
In einer geometrischen Darstellung überlappen sich die Entropien unabhängiger Ereignisse nicht.
Dies zeigt die Abbildung.
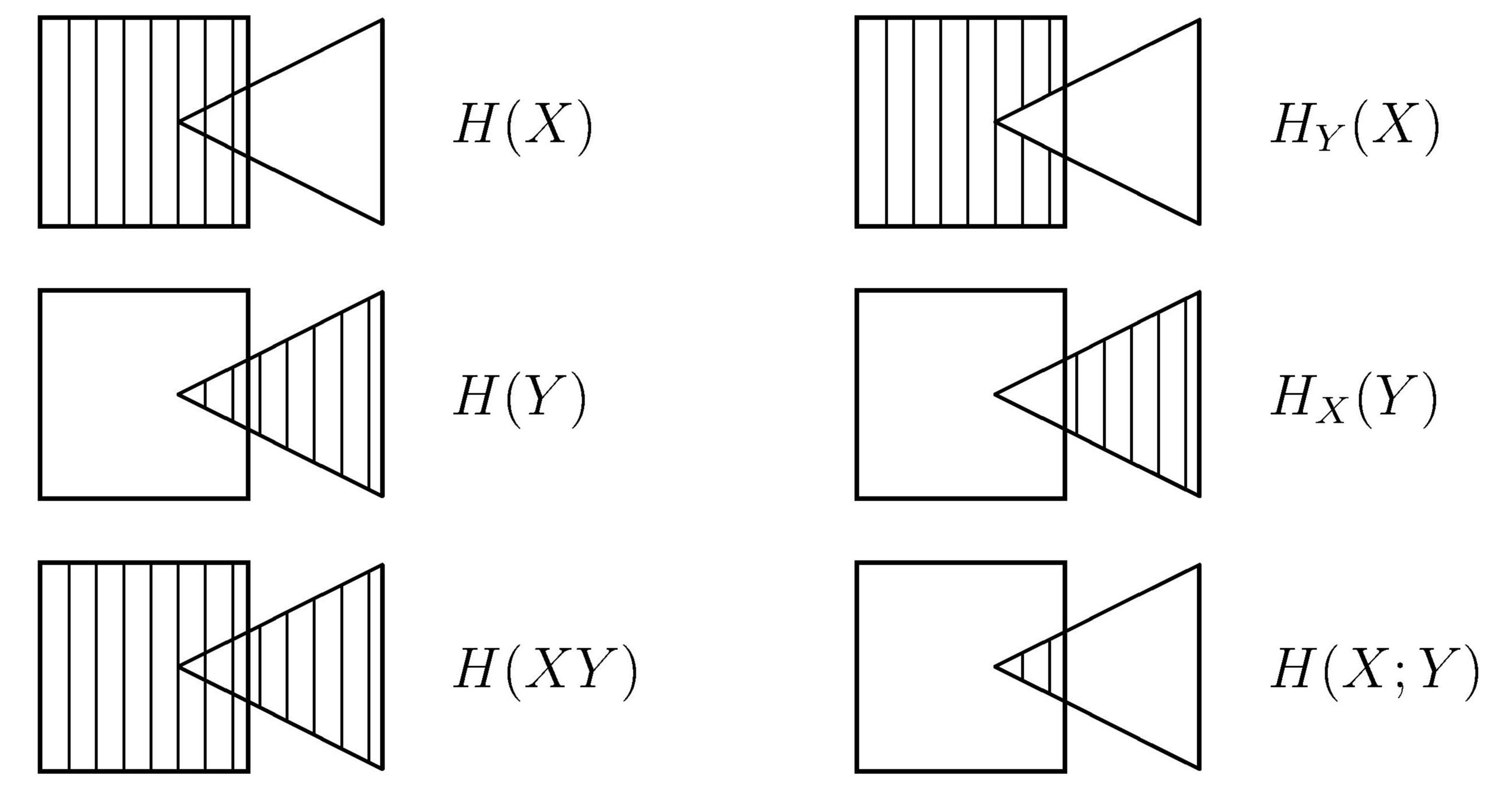
Abhängige Teilereignisse
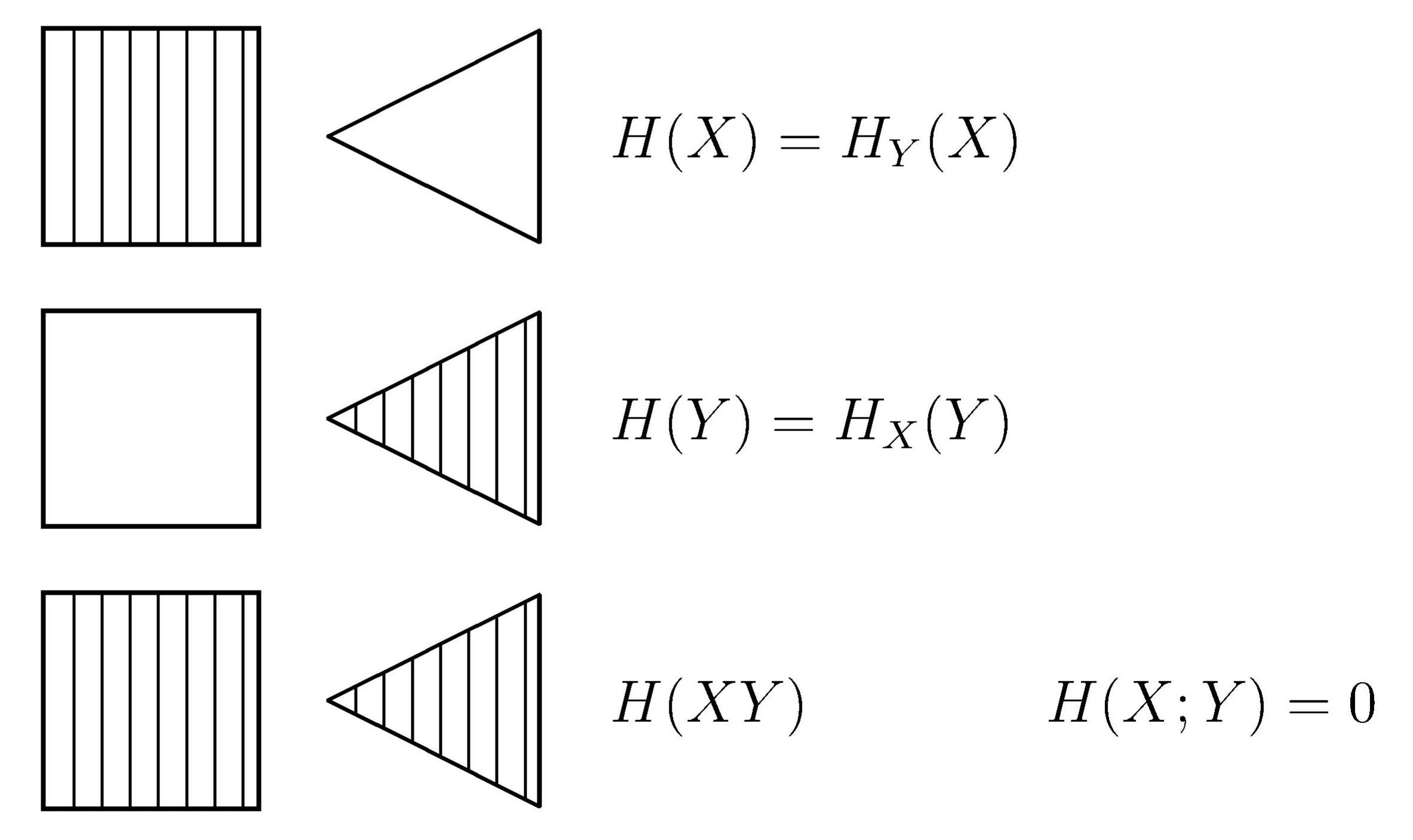
Unabhängige Teilereignisse
© Günter Green
zurück
weiter
zurück zum Anfang
1-Okt-2018