Der Übertragungskanal mit Störungen

Ein Nachrichtenübertragungskanal mit Störungen kann den Gleichungen über die Synentropie entsprechend wie in der folgenden Abbildung graphisch symbolisiert werden.

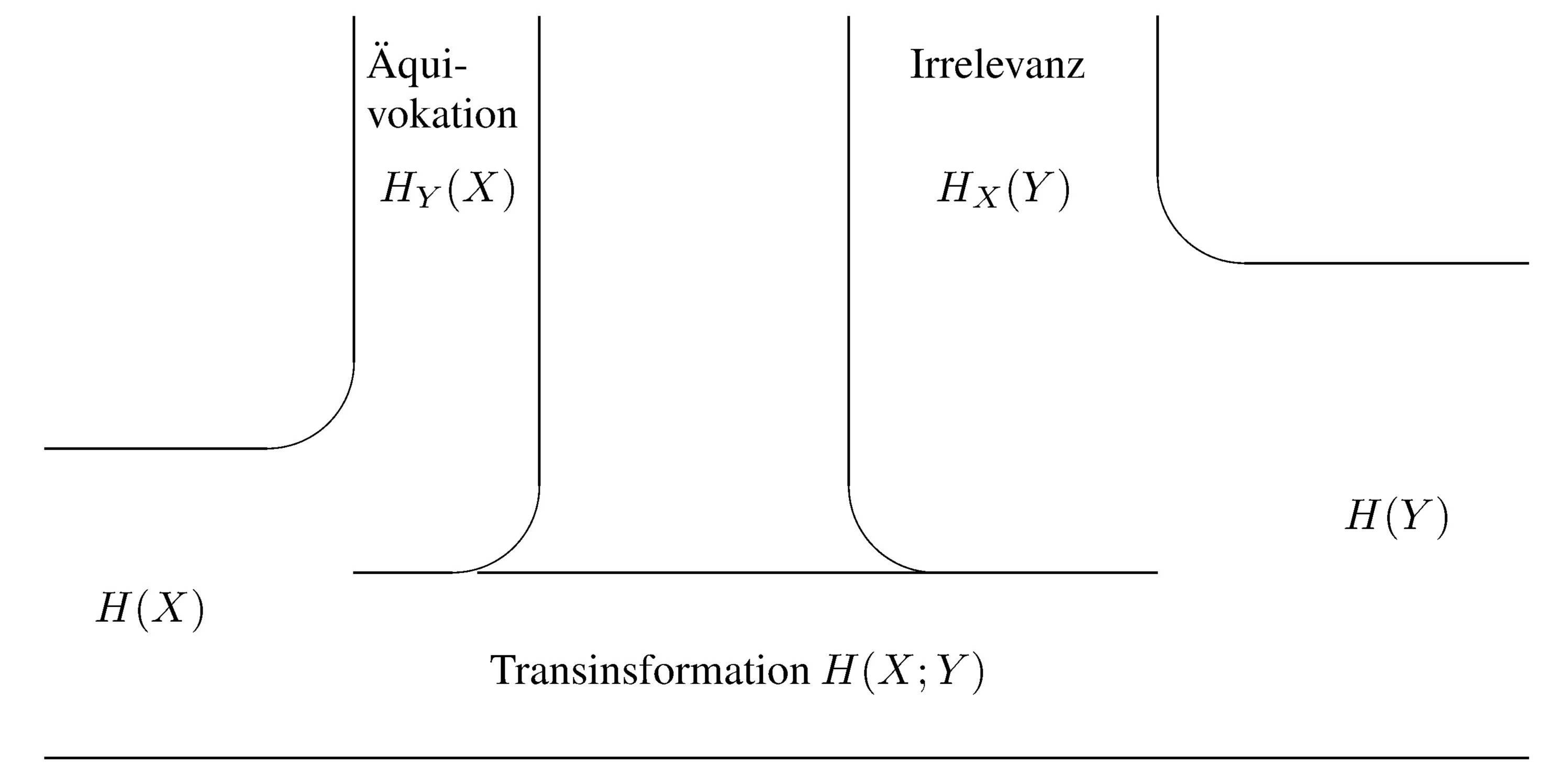
Transinformation vom Sender X zum Empfänger Y

Der Sender beliefert den Kanal aus seinem Zeichenvorrat X mit einer mittleren Information, der Sender-Entropie H(X). Wenn daraufhin der Empfänger ein Zeichen aus seinem Zeichenvorrat Y mit der Empfänger-Entropie H(Y) ausgewählt hat, verbleibt ihm wegen möglicher Störungen eine mittlere Unkenntnis H_Y(X) über das Gesendete. Sie wird als Äquivokation bezeichnet. Ebenfalls lassen Störungen eine mittlere Unvorhersagbarkeit H_X(Y), die Irrelevanz, bei der Auswahl der Empfängerzeichen zurück, nachdem irgendein Zeichen gesendet worden ist. Die im Mittel pro Zeichen übertragbare Information, die sogenannte mittlere Transinformation, ist identisch mit der bereits definierten Synentropie H(X;Y). Sie ist also gleich der Sender-Entropie H(X) abzüglich der Äquivokation H_Y(X) oder auch gleich der Empfänger-Entropie H(Y) abzüglich der Irrelevanz H_X(Y).

Ein ungestörter Kanal ist durch fehlende Äquivokation, also durch H_Y(X) = 0 gekennzeichnet, d. h. der Empfänger ist völlig sicher, welches Zeichen gesendet worden ist. Allerdings weiß der Sender nicht unbedingt, welches Zeichen er beim Empfänger ausgelöst hat. Die Transinformation H(X;Y) ist beim ungestörten Kanal im Mittel gleich der Quell-Entropie H(X).

Verschwindet die Irrelevanz, ist also H_X(Y) = 0, dann nennt man den Kanal deterministisch, d. h. der Sender weiß mit Gewißheit, welches Zeichen er beim Empfänger hervorruft.

Da aber dasselbe Zeichen von mehreren verschiedenen Senderzeichen verursacht worden sein kann, kann der Empfänger nicht unbedingt sagen, was gesendet worden ist. Die mittlere Transinformation ist in diesem Fall gleich der Empfänger-Entropie H(Y).

Ein idealer Kanal hat weder Äquivokation noch Irrelevanz, und die Transinformation ist sowohl gleich der Entropie der Quelle wie auch gleich der Entropie des Empfängers.

Kanalkapazität

Als Kanalkapazität C definieren wir dasjenige Maximum der Transinformation, das bei der dafür günstigsten Wahl (durch Kodierung) der Zeichenwahrscheinlichkeiten P der Quelle erreicht wird:

Die Kanalkapazität hängt also nicht von den Eigenschaften der Nachrichtenquelle, sondern nur von den Kanaleigenschaften ab.

Um es klarzustellen:
Transinformation und Kanalkapazität sind hier zunächst nur pro Zeichen zu verstehen. Die pro Zeit übertragbare Informationsmenge werden wir anschließend mit Hilfe des Abtastsatzes behandeln.