Der Fundamentalsatz der Kanalkodierung

Welche Bedeutung hat nun die eben definierte Kanalkapazität? Shannon's Fundamentalsatz gibt hierüber folgendermaßen Auskunft.

Ein diskreter Kanal habe die Kapazität C und eine diskrete Quelle die Entropie H pro Zeichen. Dann gilt nach Shannon (1948)

Fundamentalsatz

Für H < C gibt es eine Kodierung, die die Quellinformation mit beliebig kleiner Fehlerwahrscheinlichkeit, d. h. mit beliebig kleiner Äquivokation, überträgt.

Für H ≥ C kann durch Wahl der Kodierung die Äquivokation kleiner als H − C + ε, jedoch nicht kleiner als H − C gemacht werden.

Shannon selber hat 1948 den Beweis in der Weise skizziert, daß er nicht eine derartige Kodierungsmethode angibt, sondern zeigt, daß es eine solche Kodierung innerhalb einer gewissen Gruppe von Kodierungen geben muß. Wenn im Mittel über diese Gruppe die Äquivokation kleiner als ein vorgegebener Wert ε ist, dann muß es mindestens ein Mitglied mit einer Äquivokation kleiner als ε geben.

Wir betrachten also eine Quelle S₀ der Entropie H(X), deren Zeichenwahrscheinlichkeiten die Kanalkapazität möglichst erreicht und verwenden aus ihr Zeichenketten einer großen Länge T als Eingangssignale für den Kanal. Diese Ketten gliedern sich (siehe Quellenkodierung) in zwei Gruppen: eine hochwahrscheinliche Gruppe mit ungefähr 2^TH(X) Mitgliedern und die verbleibenden Ketten mit sehr kleiner Gesamtwahrscheinlichkeit. Faßt man auf der Empfängerseite die möglichen Zeichen ebenfalls in dieser Länge zusammen, so bestehen sie aus einer hochwahrscheinlichen Gruppe von 2^TH(Y) Mitgliedern und den übrigen mit sehr geringer Gesamtwahrscheinlichkeit.

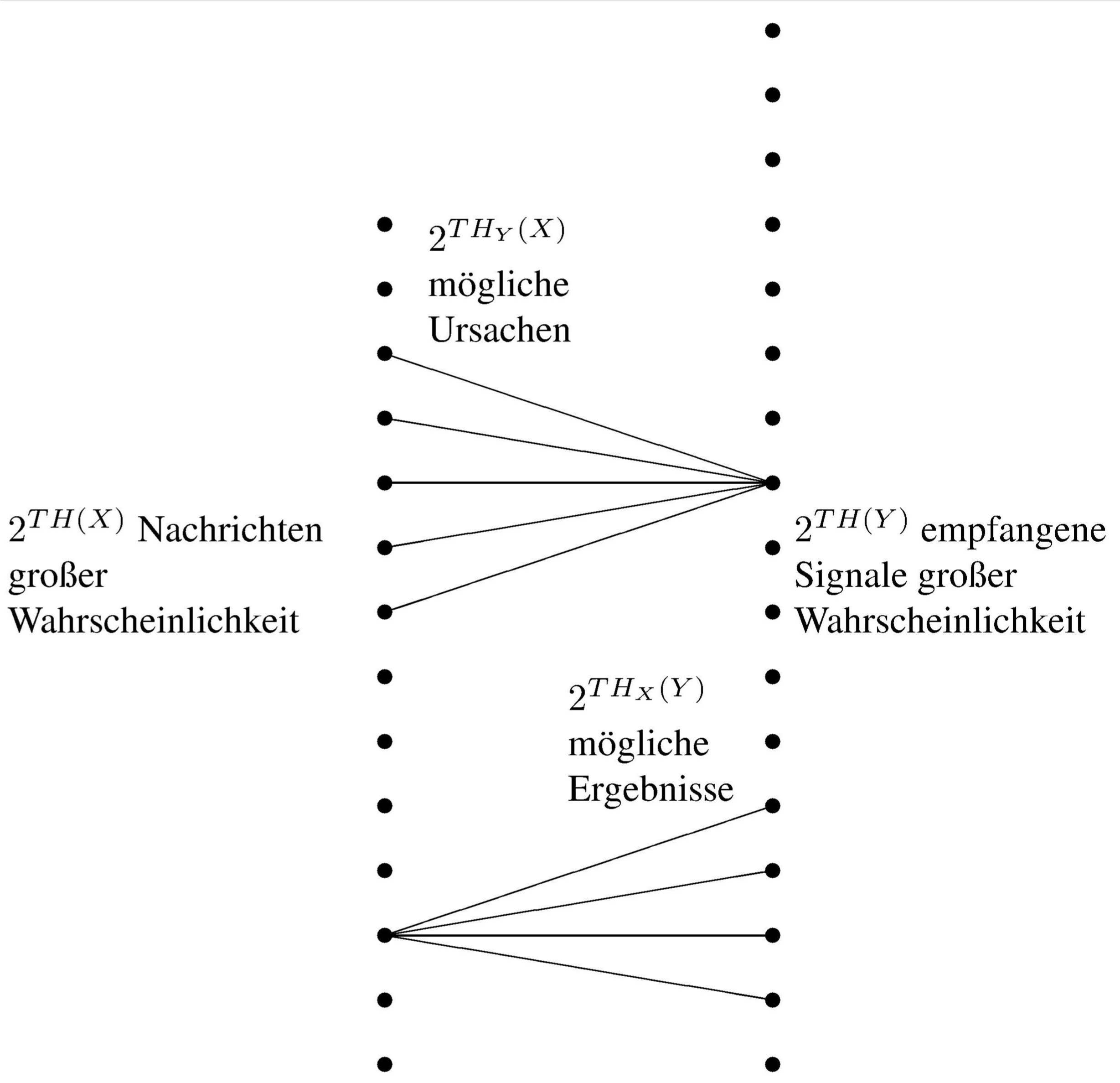
Die Zeichen dieser Quelle werden nicht fehlerfrei übertragen, denn jede empfangene Zeichenkette aus der hochwahrscheinlichen Gruppe kann wie in der folgenden Abbildung dargestellt wegen der störungsbedingten Äquivokation H_Y(X) von mehr als einer, nämlich von 2^TH_Y(X) Eingangsketten erzeugt worden sein.

links: Sender, rechts: Empfänger

Die Unsicherheit darüber, welche von diesen gleichwahrscheinlichen Ketten es gewesen ist, beträgt nämlich ld (2^TH_Y(X)) = TH_Y(X) und ist also pro Elementarzeichen auf der Empfängerseite gleich der Äquivokation H_Y(X). Ebenso kann jede hochwahrscheinliche Eingangskette wegen der störungsbedingten Irrelevanz etwa 2^TH_X(Y) Ausgangsketten erzeugen. Die Wahrscheinlichkeit aller übrigen Fälle ist insgesamt klein. Sie strebt mit wachsendem T gegen Null.

Betrachten wir jetzt aber eine andere Quelle, die pro Zeichen im Mittel nur die Information R < C in den Kanal einspeist und für die der erste Teil des Satzes also gelten soll. Hier gibt es 2^TR hochwahrscheinliche Eingangsketten der Länge T. Diese ordnen wir auf alle möglichen Weisen unter ausschließlicher Verwendung der hochwahrscheinlichen Ketten der Quelle S₀ einer Auswahl der 2^TH(X) möglichen Eingangsketten zu, d. h. wir kodieren die Eingangsketten auf alle möglichen Arten. Über diese gesamte Klasse von Kodierungen soll die Fehlerwahrscheinlichkeit gemittelt werden. Zum Zweck dieser Mittelung können wir also annehmen, daß die zu übertragenden Nachrichten diesen Zeichenketten der Länge T völlig zufällig zugeordnet sind.

Wenn nun eine spezielle Kette am Ausgang empfangen wurde, wie groß ist dann die Fehlerwahrscheinlichkeit, d. h. die Wahrscheinlichkeit, daß mehr als eine Eingangskette sie verursacht haben kann? Es sind 2^TR Nachrichten zufallsgemäß auf 2^TH(X) Punkte in der obigen Abbildung verteilt. Die Wahrscheinlichkeit P_N, daß ein bestimmter Punkt eine Nachricht ist, ist daher

Die Wahrscheinlichkeit für fehlerfreie Übertragung, dafür also, daß keiner der Punkte (außer der ursprünglichen Nachricht) eine Nachricht ist, beträgt

Da nun R < C ≡ H(X) − H_Y(X) und somit R − H(X) = −H_Y(X) − η mit positivem η sein soll, ist die Wahrscheinlichkeit für fehlerfreie Übertragung

Mit wachsendem T strebt dieser Ausdruck, also die Wahrscheinlichkeit für fehlerfreie Übertragung, gegen Eins.

Für den Logarithmus von P gilt nämlich mit wachsendem T wegen ln (1 − x) → −x für x → 0

Damit ist die erste Hälfte des Satzes bewiesen.

Zum Beweis der zweiten Hälfte nehmen wir an, daß wir im Mittel von der Quellinformation H(X) nur einen beliebigen Anteil der Größe C senden, was wegen des ersten Teils des Satzes mit beliebig kleiner Äquivokation möglich ist. Zu diesem beliebig kleinen Äquivokationsbeitrag kommt dann auf der Empfängerseite wegen des weggelassenen Teils die Äquivokation H_Y(X) = H(X) − C hinzu.

Der Kanalkodierungssatz zeigt, was man bei vorgegebenen Störungen durch eine geeignete Kodierung erreichen kann, nämlich:

Man kann mit beliebig kleiner Fehlerwahrscheinlichkeit Information übertragen, wenn die mittlere Information pro Zeichen unter einer bestimmten Grenze bleibt. Anders als man befürchten könnte, muß also mit zunehmenden Störungen nicht auch eine zunehmende Fehlerhäufigkeit verbunden sein.
Dies gilt insbesondere auch dann, wenn die Zeichenwahrscheinlichkeiten der Quelle nicht auf maximale Transinformation zugeschnitten sind. Hierzu ist eine an die Störungen angepaßte Kodierung erforderlich.

Wie die Kodierung tatsächlich zu gestalten ist, deutet der Satz nur an. Diese Frage ist Gegenstand der Kodierungstheorie und soll hier nicht behandelt werden. Er zeigt aber klar, was durch Kodierung zu erreichen und was nicht zu erreichen ist.

Daß wir den Kanalkodierungssatz hier nur für diskrete Kanäle betrachtet haben, bedeutet insofern keine wesentliche Einschränkung, als reale kontinuierliche Kanäle wegen beschränkter Amplitudenauflösung diskretisiert betrachet werden können. Tatsächlich wird in der Praxis hiervon durch Analog-Digital-Wandlung zunehmend auch technisch Gebrauch gemacht.