Einteilung von Übertragungskanälen
Übertragungskanäle lassen sich nach verschiedenen Merkmalen einteilen.
Je nachdem, ob die Ein- und Ausgangszeichen aus einem diskreten
oder einem kontinuierlichen Raum gewählt werden, bezeichnet man Kanäle als
diskret oder kontinuierlich.
Im kontinuierlichen Falle können die Zeichen zeitdiskret oder zeitkontinuierlich gewählt werden.
Entsprechend wird der Kanal zeitdiskret oder zeitkontinuierlich genannt.
Aufgrund der bedingten Wahrscheinlichkeitsverteilung, die die Zuordnung
zwischen Ein- und Ausgangszeichen bestimmt, unterscheiden wir Kanäle
ohne und mit Gedächtnis.
Bei den letzteren hängt diese Verteilung von den vorangehenden Zeichen ab.
Bei konstanten Kanälen ist die Verteilung für alle
aufeinanderfolgenden Paare von Ein- und Ausgangsereignissen dieselbe.
Eine etwas ausführliche Einteilung von Übertragungskanälen findet man
z. B. bei Fano (1966).
Diskrete konstante Nachrichtenkanäle lassen sich
anhand der Kanalmatrix klassifizieren.
Eine solche Matrix mit den Elementen (siehe das
Beispiel)
die nicht von den Eigenschaften des Senders oder des Empfängers abhängt,
gibt an, mit welcher Wahrscheinlichkeit ein Zeichen yk aus dem
Zeichenvorrat Y des Empfängers
durch ein Eingangszeichen xi aus dem
Zeichenvorrat X des Senders hervorrufen wird.
Sie verknüpft die Wahrscheinlichkeiten der Ausgangszeichen mit denen der Eingangszeichen,
je als Zeilenvektor geschrieben, durch
Wenn auf jedes Eingangszeichen mit Sicherheit irgendein Ausgangszeichen folgt,
dann sind die Zeilensummen der Kanalmatrizen gleich Eins.
Die Kanalmatrizen sind dann sogenannte
stochastische Matrizen.
Beispiel:
Der Sender habe das binäre Alphabet {0,1}, das Empfängeralphabet sei {A,B,C}, und die Kanalmatrix sei
Sie ordnet der Eingangsverteilung
durch Multiplikation mit der Kanalmatrix K die Ausgangsverteilung
zu.
Die Kanalmatrix beschreibt in diesem Beispiel einen ungestörten,
aber keinen deterministischen Kanal,
denn aus jedem Ausgangszeichen kann eindeutig auf das Eingangszeichen rückgeschlossen werden,
da in jeder Spalte genau ein von Null verschiedenes Element steht.
Der Kanal ist also äquivokationsfrei.
In der entgegengesetzten Richtung ist die Übertragung nicht eindeutig bestimmt,
weil in der ersten Zeile zwei positive Elemente stehen.
Hierin steckt die Irrelevanz.
Bei einem deterministischen Kanal hat die Kanalmatrix in jeder Zeile genau eine Eins.
Es können aber in jeder Spalte mehrere Einsen stehen.
Steht in jeder Spalte und, weil die Matrix stochastisch ist,
auch in jeder Zeile genau eine Eins, dann ist der Kanal ideal.
Sind alle Zeilen Permutationen der ersten Zeile, dann nennt man den Kanal
vom Eingang her gleichförmig oder uniform,
weil die auf das Einzelzeichen bezogene
Irrelevanz Hxi(Y)
für alle Senderzeichen xi
gleich und damit gleich der
über alle Senderzeichen gemittelten Irrelevanz HX(Y) ist.
Denn die Summe über die i-te Zeile der Kanalmatrix ist bis auf
Vertauschungen der Summanden für alle Zeilen und damit für alle
Eingangszeichen xi gleich.
Die Übertragung eines jeden der möglichen Eingangszeichen wird also im
gleichen Maße durch das Kanalrauschen gestört.
Sind darüber hinaus alle Spalten der Kanalmatrix Permutationen der ersten Spalte,
dann heißt der Kanal doppelt uniform.
Sind alle Zeilen identisch, haben wir es mit einem total gestörten Kanal zu tun.
Der Empfänger hat dann keine Hinweise mehr auf das gesendete Signal.
Die Verbundwahrscheinlichkeiten p(xiyk)
ergeben sich als Produkt der
Wahrscheinlichkeiten p(xi) der Senderzeichen
mit den Elementen der Kanalmatrix:
p(xiyk) =
p(xi) pxi(yk).
Auf der Senderseite mögen die beiden Zeichen 0 und 1
mit den Wahrscheinlichkeiten p0
und 1 − p0 auftreten.
Der Empfänger habe den gleichen Zeichenvorrat.
Die Kanalmatrix ist dann quadratisch.
Der Kanal unterliege Störungen, und zwar – wie die folgende Abbildung zeigt – so,
daß aus einem gesendeten Binärzeichen mit der Wahrscheinlichkeit p das entsprechende Zeichen
und mit der Wahrscheinlichkeit 1 − p
das falsche Zeichen empfangen wird.
Die Störungen sollen sich also symmetrisch auf beide Binärzeichen (daher der Name) auswirken.
Im obigen Sinne ist der Kanal uniform.
Wieviel Information kann nun ein solcher Kanal pro Zeichen übertragen?
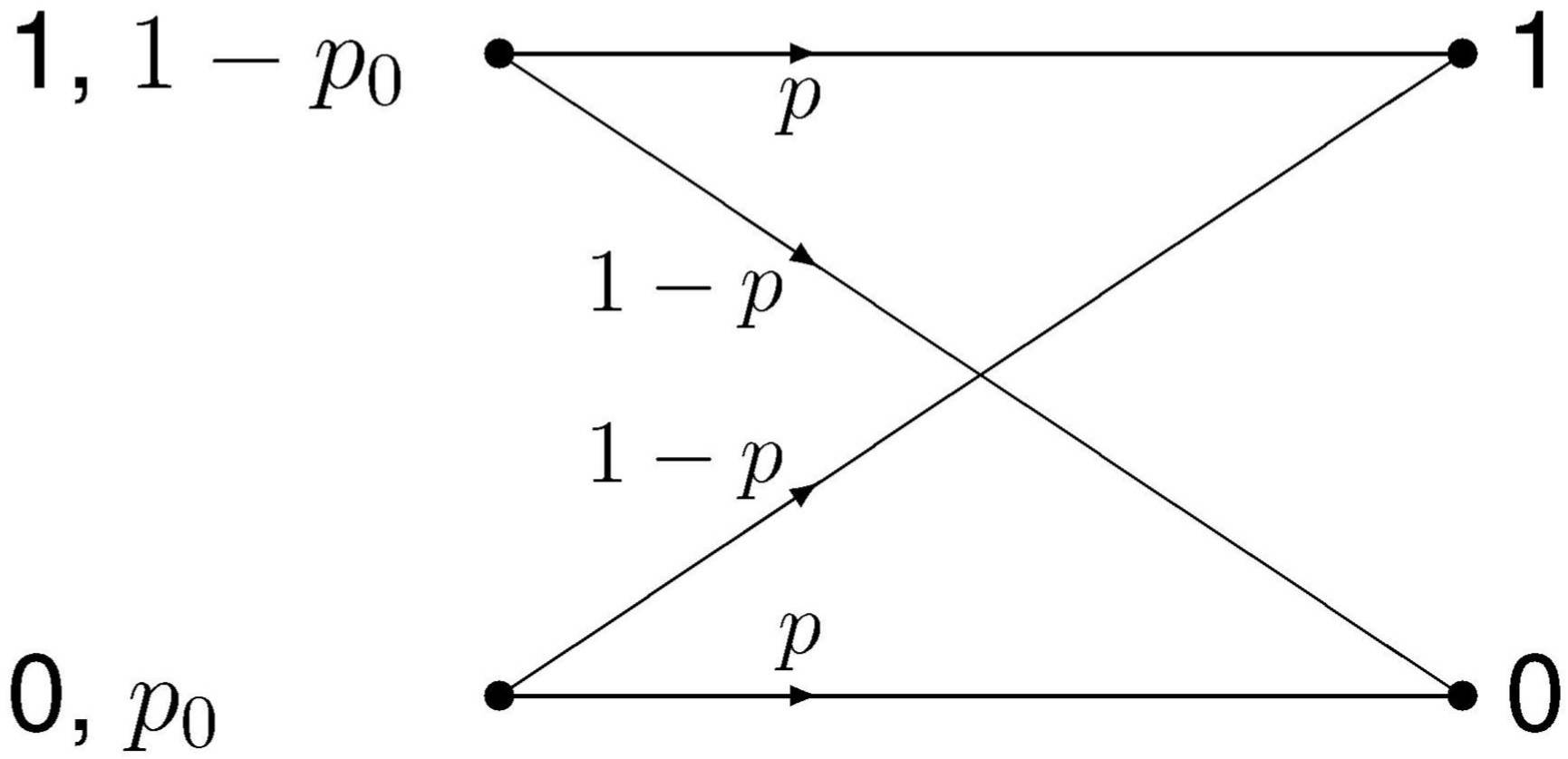
links: Sender, rechts: Empfänger
Nehmen wir etwa an, p sei 0.5,
d. h. im Mittel werde jedes zweite Zeichen in das komplementäre Zeichen verfälscht.
Man könnte dann spontan glauben, pro Zeichen würden 0.5 bit übermittelt,
da ja jedes zweite Zeichen richtig übertragen wird.
Das ist falsch, denn der Empfänger weiß nicht, welches die ver\-fälsch\-ten Zeichen sind.
Um die pro Zeichen tatsächlich übertragbare Information zu finden, müssen
wir die mittlere Transinformation für diesen Kanal berechnen.
Seine Kanalmatrix mit den
Elementen pxi(yk) lautet
und die Matrix der Verbundwahrscheinlichkeiten
p(xiyk) =
p(xi) pxi(yk)
ist
Beim Empfänger erscheint gemäß der Kanalmatrix
das Zeichen yk mit der Wahrscheinlichkeit
Die Empfängerzeichenwahrscheinlichkeit q(yk) ist also die k-te
Spaltensumme der Matrix der Verbundwahrscheinlichkeiten p(xiyk).
Beim binärsymmetrischen Kanal ist also
Die Entropien
lassen sich durch die Shannon-Funktion S ausdrücken:
Hieraus ergibt sich die mittlere Transinformation
Die mittlere Transinformation des binärsymmetrischen Kanals ist als
Funktion der Quellwahrscheinlichkeit p0 und der Kanalwahrscheinlichkeit p
in der folgenden Abbildung dargestellt.
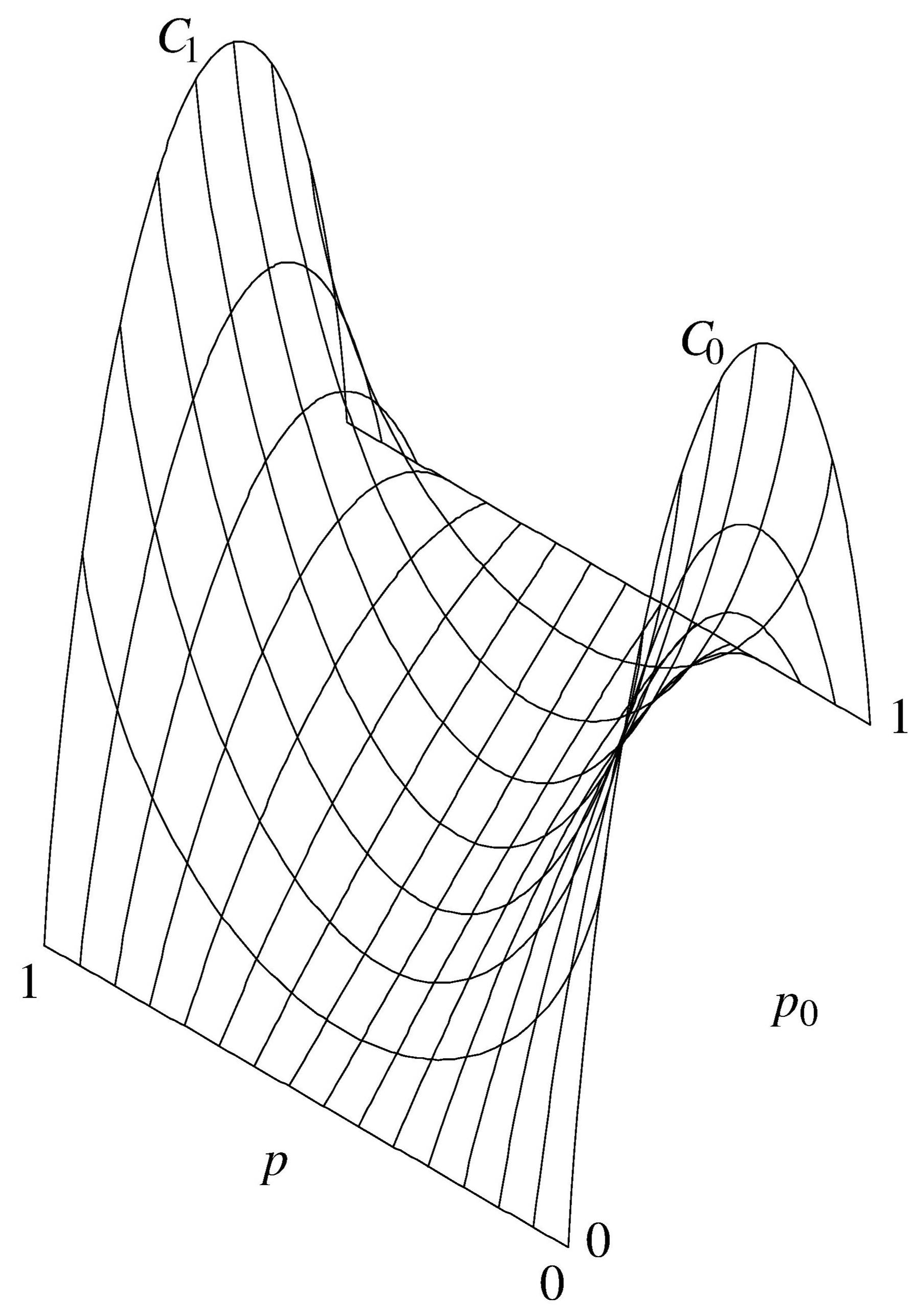
Mittlere Transinformation beim binärsymmetrischen Kanal
Sie bildet eine sattelförmige Fläche.
Die Kanalkapazität des binärsymmetrischen Kanals
als Maximum der Transinformation bei günstigster Wahl der Wahrscheinlichkeiten
der Senderzeichen ist, wie die Abbildung zeigt,
gleich der Transinformation in der Ebene p0 = 0.5.
Betrachten wir drei Spezialfälle.
-
p0 = 0

Wird ausschließlich das Zeichen 1 gesendet, kann also keine Information übertragen werden.
Genauso wenig geht das, wenn p0 = 1 ist.
-
p0 = 0.5

Bei dieser günstigsten Verteilung der senderseitigen Zeichenwahrscheinlichkeiten
kann man also pro Binärzeichen 1 bit an Information übertragen,
wenn der Kanal jedes Zeichen richtig übermittelt (p = 1).
Man kann es aber auch, wenn er kein einziges Zeichen richtig wiedergibt (p = 0).
Denn wenn dieser Tatbestand dem Empfänger bekannt ist,
braucht er nur regelmäßig 0 und 1 zu vertauschen.
-
Wir können jetzt auch den eingangs betrachteten Fall korrekt berechnen.
Wenn im Mittel jedes zweite Bit falsch übertragen wird (p = 0.5), dann ist die
mittlere Transinformation 1 − S(0.5) = 0 ,
und es ist tatsächlich überhaupt keine Information übertragbar.
Untersucht werden soll, wieviel Information im Mittel in einem Amplitudenwert übertragen werden kann.
Wir betrachten also zunächst noch keine Zeitfunktion, sondern nur einen Momentanwert.
Wir wollen mit x das Eingangssignal und mit y das Ausgangssignal eines
kontinuierlichen Nachrichtenübertragungskanals bezeichnen.
Die Wahrscheinlichkeitsdichte des Verbundereignisses xy ist
p(xy) = p(x) px(y)).
Die bedingte Wahrscheinlichkeitsdichte px(y) entspricht der Kanalmatrix bei diskreten Kanälen.
Ein idealer kontinuierlicher Kanal ist gekennzeichnet durch
px(y) = δ(y − x).
Jedem x wird umkehrbar eindeutig ein y zugeordnet.
In der Praxis unterliegen kontinuierliche Kanäle Störungen unterschiedlichster Art und Stärke.
Jeder kennt dies bei Telefonverbindungen, beim Rundfunk- und Fernsehempfang und
bei Magnetband- und Schallplattenaufnahmen.
Wir wollen uns hier darauf beschränken,
eine spezielle häufig auftretende Art von Störungen zu betrachten,
nämlich additives Rauschen,
also ein Signal, das sich unabhängig von der Signalamplitude ihr störend überlagert.
Nichtlineare Verzerrungen
wären z. B. keine additiven Störungen,
da sie von der Nutzamplitude abhängen.
Additivität des Rauschens bei einem kontinuierlichen Kanal ist analog zur
Gleichförmigkeit vom Eingang her bei einem diskreten Kanal.
Das Ausgangssignal y bestehe also aus dem Eingangssignal x,
zu dem sich von x unabhängige Störungen z addieren:
y = x + z
Die bedingte Wahrscheinlichkeitsdichte px(y) kann dann als Funktion
der Störungen allein beschrieben werden:
px(y) = q(z).
Hieraus läßt sich zunächst
als bedingte Entropie HX(Y) die Irrelevanz,
also die mittlere Unbestimmtheit des Empfängerzeichens
nach Aussendung eines Senderzeichens, berechnen:
Wir erhalten daraus die mittlere Transinformation
H(X;Y) = H(Y) − HX(Y)
= H(Y) − H(Z).
Hier wird die schon diskutierte Frage des Koordinatensystems aktuell.
Betrachten wir einen idealen kontinuierlichen Kanal,
dann könnte
H(
Z) unendlich negativ werden, und es schiene,
als ob die mittlere Transinformation über alle Grenzen wüchse,
selbst wenn die Quelle nur eine endliche Entropie besitzt.
Für eine realistische Beschreibung ist hier aber wiederum
bei
px(y) der δ-Funktion
ein schmales Rechteck anzusetzen,
dessen Breite ε das Auflösungsvermögen der Übertragungsapparatur repräsentiert.
Das Koordinatensystem kann so gewählt werden, daß
H(
Z) gerade gleich Null wird.
Die mittlere Transinformation wird dann gleich der Empfängerentropie
H(
Y).
Ist
p(
y) z. B. eine Rechteckverteilung
im Intervall [y
1,y
2] = [x
1,x
2],
dann ist die Transinformation
Diese Wahl macht die Verhältnisse zwar besonders übersichtlich,
jedoch sind wir nicht auf dieses spezielle Koordinatensystem angewiesen,
denn die mittlere Transinformation ist, wie wir schon gesehen hatten,
als Differenz zweier Entropien von der Wahl des Koordinatensystems unabhängig.
© Günter Green
zurück
weiter
zurück zum Anfang
22-Sep-2018


