Kontinuierliche Zeitfunktionen

Man kann folgende Arten von Zeitfunktionen unterscheiden:

deterministisch
- periodisch
  - sinusförmig, z. B. cos(ω t − φ)
  - komplex periodisch, z. B.
- nichtperiodisch
  - fast periodisch, z. B. , wobei ω_n/ω_m nicht rational ist
  - Übergangsfunktionen (Transienten), z. B. H(t) e^{−t /τ}
nichtdeterministisch (Zufallsfunktionen)
- stationär
  - ergodisch
  - nicht ergodisch
- nicht stationär
  - spezielle Fälle

Im Rahmen der Informationstheorie befassen wir uns vorrangig mit nichtdeterministischen Funktionen, da der Verlauf deterministischer Funktionen vorhersagbar ist und keine Information liefert.

Kontinuierliche Zeitfunktionen von beschränkter Bandbreite lassen sich, wie wir in dem folgenden Shannonschen Abtastsatz (engl. sampling theorem) sehen werden, ohne Informationsverlust durch zeitlich diskrete Abtastwerte darstellen. Eine solche Funktion muß also keineswegs kontinuierlich vermessen werden. Vielmehr reicht pro Zeiteinheit eine endliche Zahl von Funktionswerten aus. Wenn außerdem ihre Amplituden mit nur endlicher Genauigkeit vorliegen, dann enthält die Funktion nur endlich viel Information pro Zeiteinheit.

Der Abtastsatz kann auf verschiedene Weise hergeleitet werden, von denen hier zwei gezeigt werden sollen.

Der Abtastsatz

Die erste Herleitung stützt sich auf Bendat-Piersol (1971). Eine frequenzbandbegrenzte Zufallsfunktion x(t) habe die Fourier-Transformierte X(f). Diese sei Null außerhalb des Intervalls [−B,B]. Es gilt daher

Denkt man sich das Spektrum X(f) mit der Periode 2B wiederholt, dann läßt es sich als Reihe

schreiben mit den Koeffizienten

Sie ergeben sich aus der Orthogonalität dieser Exponentialfunktionen im Intervall [−B,B].

Diese Reihe beschreibt das Spektrum dann auch im Intervall [−B,B], innerhalb dessen es im folgenden nur verwendet wird. Da die Zeitfunktion an der Stelle t = n/(2B) gleich

ist, können, wie der Vergleich mit dem voranstehenden Ausdruck für c_n zeigt, die Koeffizienten c_n durch äquidistante Abtastwerte ausgedrückt werden:

Für das Spektrum gilt damit

Setzt man dieses Spektrum in die frequenzbandbeschränkte Zeitfunktion ein, dann wird sie

Damit erhält man den Abtastsatz:

Ein auf das Frequenzband [−B,B] beschränktes Signal ist vollständig bestimmt durch äquidistante Stützstellen im Abstand 1/(2B).

Die Stützwerte sind Koeffizienten einer Reihenentwicklung nach dem Funktionensystem

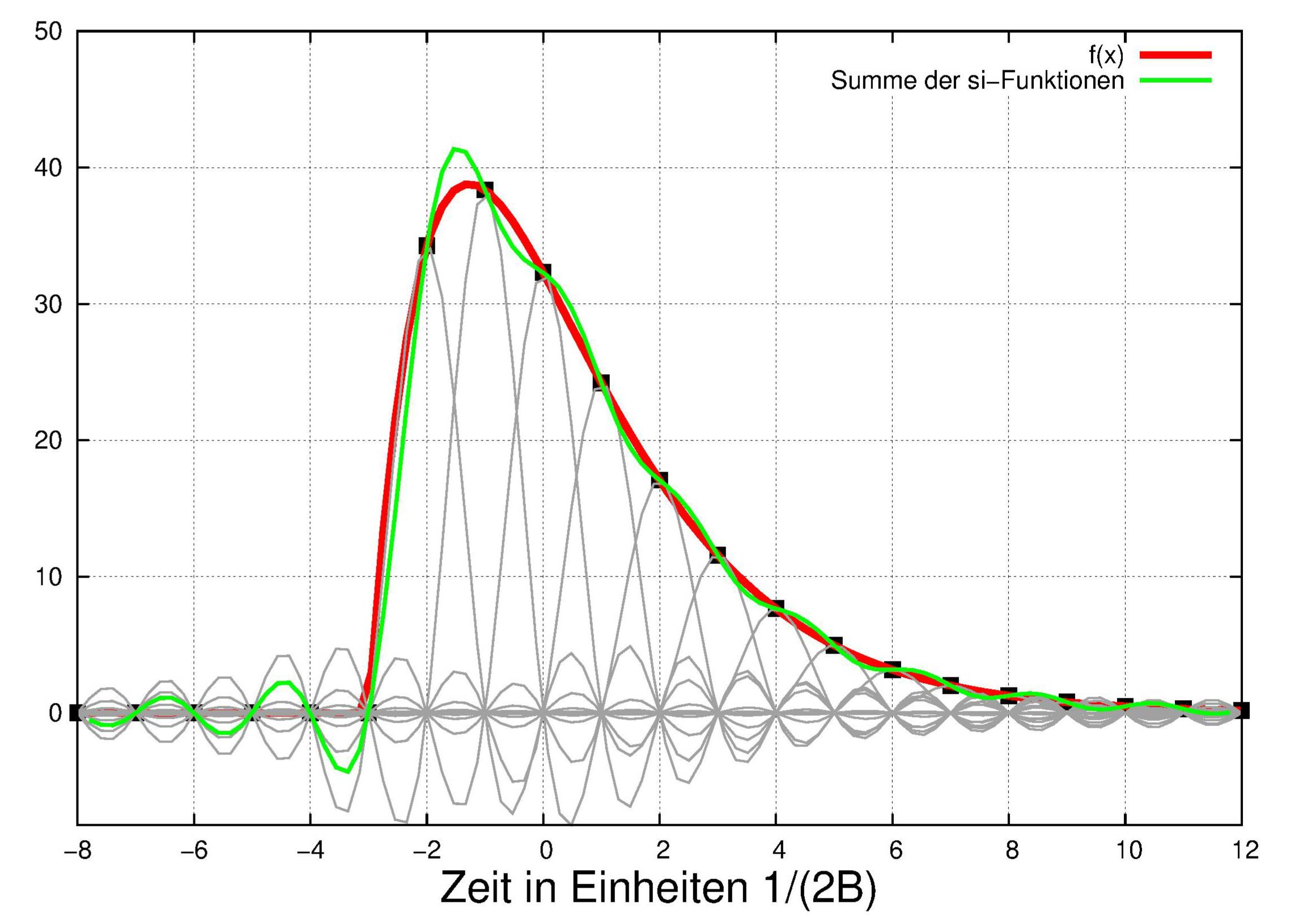
und liegen in den absoluten Maxima der um n/(2B) verschobenen si-Funktionen. Dort ist genau eine von ihnen, nämlich y_n(t), gleich Eins, während alle anderen dort Nullstellen haben. Eine solche Reihe, bei der nur einige benachbarte Abtastwerte von Null verschieden gewählt sind, ist in der folgenden Abbildung dargestellt.

Wenn man den Abtastsatz auf die (sicherlich frequenzbandbeschränkte) konstante Funktion x(t) = 1 anwendet, ergibt sich für das orthogonale si-Funktionensystem bei jeder Bandbreite B:

Eine zweite Herleitung des Abtastsatzes findet sich bei Fischer (1969}: Mit Hilfe der Integraldarstellung

Man bestätigt sie, indem man die Integration durchführt und die Exponentialschreibweise der sin-Funktion und (si(x) ≡ sin(x) / x benutzt..

der si-Funktion

erhält man zunächst die Orthogonalität des Funktionensystems y_n(t) im beidseitig unendlichen Intervall:

Schreibt man eine auf das Frequenzband [−B,B] begrenzte Zeitfunktion x(t) als Reihe

multipliziert mit 2B y_n(t) und integriert von ±B bis B, so erhält man wegen der Orthogonalität der y_n(t) mit der obigen Integraldarstellung der si-Funtion) für die Koeffizienten

Damit sind (siehe (\ref{eq:abt1})) die Koeffizienten

Die Integrationsgrenzen konnten hierin von ±B auf ±∞ erweitert werden, weil wir voraussetzen, daß das Spektrum X(f) außerhalb B Null ist. In der letzten Zeile steht dann die als Fourier-Integral geschriebene Zeitfunktion x(t) an der Stelle t = n/(2B). Mit diesen Koeffizienten ergibt sich wiederum der Abtastsatz als

Die für die Anwendung des Abtastsatzes erforderliche strenge Bandbegrenzung ist nicht immer von vornherein gegeben. Sie muß dann durch ein Tiefpaßfilter gewährleistet werden. Es hat im Idealfall eine unendlich steile Flanke bei der Frequenz B. Flachere Flanken hätten die unerwünschte Folge, daß die Signalamplitude bereits bei niedrigeren Frequenzen gedämpft wird. Filter mit sehr steilen Flanken erfordern allerdings einen erheblichen Aufwand.

Hält man die Bandbegrenzung nicht streng ein, dann enthalten die Abtastwerte irreführende Information, so daß die daraus zu rekonstruierende kontinuierliche Zeitfunktion drastisch verfälscht werden kann. Je weiter die Grenze B überschritten wird, um so mehr überlappen sich die periodischen Fortsetzungen des Spektrums und bei um so tieferen Frequenzen erscheinen solche Beiträge bei der Wiedergabe. Man nennt diesen Effekt im Englischen `Aliasing'.

Er entspricht der Erscheinung, daß rollende Speichenräder bei Kinofilmen sich fälschlich rückwärts zu drehen scheinen, wenn weniger als zwei Bilder pro Speichenperiode aufgenommen werden.

Rekonstruktion einer Funktion aus Abtastwerten

Die ursprüngliche Funktion kann man aus den Abtastwerten rekonstruieren, indem man eine Folge von schmalen Rechteckimpulsen in den Abtastpunkten verwendet, deren Flächen proportional zu den Abtastwerten sind, und durch ein Tiefpaßfilter mit rechteckiger Durchlaßkurve alle Frequenzanteile oberhalb B abschneidet. Ein solches Filter macht aus genügend schmalen Rechteckimpulsen nämlich die si-Funktionen, die in der obigen Reihe benötigt werden.

Betrachten wir hierzu einen Abtastwert der Höhe A. Wir ordnen ihm einen Rechteckimpuls der Höhe A/(2 B ε) zu, der sich von −ε/2 bis ε/2 erstreckt. Er hat das Spektrum

Dieses Spektrum schneiden wir außerhalb B durch ein Filter ab. Je kleiner die Breite ε des Rechteckimpulses ist, um so breiter ist die si-Kurve und um so mehr nähert sich das verbleibende Spektrum einem ebenfalls rechteckigen Verlauf an. Die Breite ε ist dabei nicht sehr kritisch. Ist das Tastverhältnis der Rechteckimpulse 0.5, ihre Breite bei einer Abtastperiode 1/(2B) also ε = 1/(4B), dann hat das Spektrum an der Filtergrenze B noch 90 Prozent seines Maximalwertes A/(2B)) bei f = 0. Selbst wenn die Rechteckimpulse ihre maximal mögliche Breite ε = 1/(2B) annehmen, bei der sie sich lückenlos an ihre Nachbarn anschließen, ist die si-Funktion dort nur auf 63 Prozent gesunken. Für schmalere Impulse können wir daher mit guter Näherung ein rechteckiges Spektrum von −B bis B annehmen. Ihm entspricht die Zeitfunktion

also genau der gewünschte nullte Term der Reihe mit dem Abtastwert A als Koeffizienten.

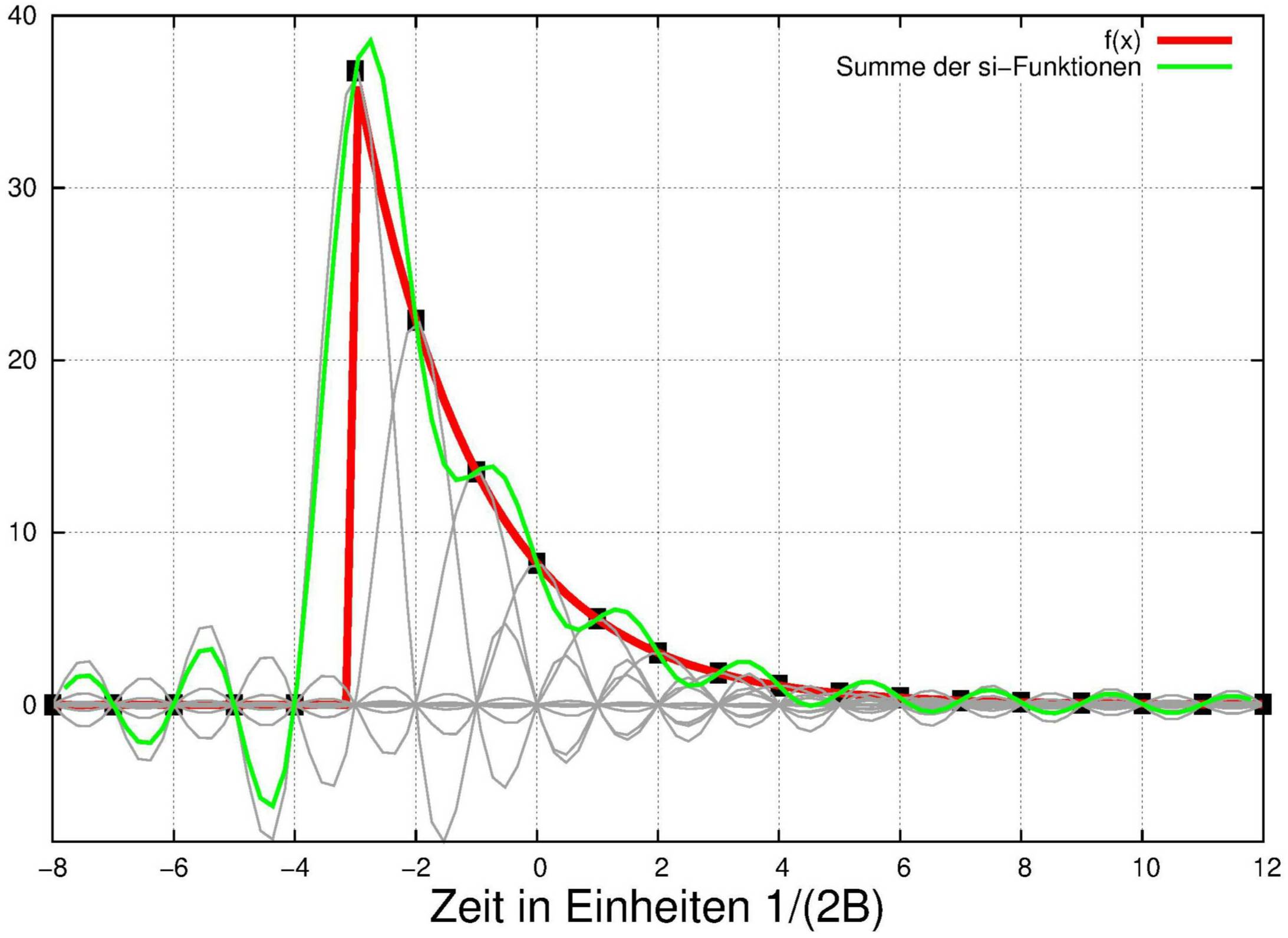
Die Überlagerung dieser Terme wie in der vorigen und der folgenden Abbildung ist das rekonstruierte Signal.

Hier hat das Signal (rot) wegen des steilen Anstiegs einen höheren Anteil von Frequenzen außerhalb der Bandbreite, die dem Abtasten entspricht. Dadurch weicht das rekonstruierte Signal (grün) hier mehr vom Original ab als bei dem rundlicher ansteigenden Signal in der vorigen Abbildung.

Einen zum hier behandelten Abtastsatz dualen Satz kann man formulieren und beweisen, indem man Zeit und Frequenz vertauscht.