Über die Abplattung der Erdkugel

Läßt sich die Abplattung der Erdkugel aus den bekannten Formeln für Gravitation und Fliehkraft theoretisch herleiten? Oder sind dazu weitere Bedingungen erforderlich?

Eine Antwort findet man bei Fitzpatrick unter 'Rotational Flattening'.

Ich will unabhängig davon versuchen, diese einfachklingende Frage hier zu beantworten.

Die Erde als Kugel

Bereits der griechische Philosoph Pythagoras (570 – 510 v. Chr.) und seine Schüler gingen von einer Erdkugel aus – das war im 6. Jahrhundert, vor Christus wohlgemerkt.
Die Griechen gingen schon lange vor Eratosthenes von einer Kugelgestalt der Erde aus. Bereits Aristoteles (384 – 322 v. Chr.) befasste sich mit der Frage ihres Umfangs.
Eratosthenes, der etwa von 276 bis 194 vor Chr. lebte, war der erste, der den Umfang der Erde berechnet hat - und dies setzt voraus, dass die Erde keine Scheibe, sondern eine Kugel ist.

Bereits einige Jahre bevor Hekataios seine Erdkarte zeichnete, entstand allerdings schon der Gedanke, die Erde sei eine Kugel. Er tauchte seit Pythagoras, einem Philosophen und Mathematiker aus Samos, immer wieder auf, konnte sich jedoch gegenüber den herrschenden Lehren der Priester, wonach die Erde eine Scheibe war, nicht durchsetzen. Erst etwa 200 Jahre später wurden u. a. von Aristoteles indirekte Beweise für die Kugelgestalt angeführt:
Erst Christoph Kolumbus habe als einer der ersten Menschen an die Kugelgestalt der Erde geglaubt.
(Quelle)

Vermessung der Erdkugel

Die erste wirklich genaue Erdmessung geht auf die 1666 gegründete Pariser Akademie zurück, die um 1730 entschied, zwei geodätische Expeditionen nach Peru (heutiges Ecuador, 1735–1744) und nach Lappland (1736–1737) zu entsenden.

Bei Messungen der Erdfigur ergab sich, daß der Radius am Äquator mit 6378 km um 21.38 km länger ist als die Radien an den Polen mit 6357 km. Die Erdkugel ist also etwas abgeplattet und nimmt in nächster Näherung die Formeines Rotationsellipsoids an. Örtliche Abweichungen davon wie Gebirge seien hierbeiunberücksichtigt.

Ursache der Abplattung

Auf ein Massenelement eines Himmelskörpers wirken, wenn man vom Einfluß benachbarter Himmelskörper absieht, zwei verschiedene Kräfte:

die Gravitation, nämlich die Massenanziehung durch alle anderen Massenelemente des Körpers,
die Fliehkraft, wenn der Körper gegenüber dem Fixsternhimmel rotiert.

Abb.1: Die Gravitation wirkt nahezu kugelsymmetrisch, hier im Bild von den roten Punkten in Richtung auf den Erdmittelpunkt. Die (schwächere, aber hier zur Demonstration um einen Faktor 100 erhöhte) Fliehkraft wirkt von den grünen Punkten im rechten Winkel zur hier waagerecht gezeichneten Erdachse zu den blauen Punkten nach außen. Die Summe beider Kräfte (schwarze Linien) ist erdeinwärts gerichtet mit einer Tendenz zum Äquator (oben und unten) in der Zeichnung. Zu beiden Kräften gehört je ein Potential.

Herleitung der Radiendifferenz

Dies ist ein mehrere hundert Jahre altes Problem, das schon Newton (1642 – 1727) vor mehr als dreihundert Jahren in seinen Principia (1686) beschäftigt hat. Allerdings ist dort nicht zu erkennen, welche physikalischen Gesetze er zugrundegelegt hat. Auch Chandrasekhar (1888 – 1970) hat dieses Thema behandelt. Zwar stellt er Zahlenwerte für die Radiendifferenz vor, aber auch er läßt die physikalischen Gesetze unerwähnt, auf denen seine Rechnungen basieren.

Modelle, die die Gleichgewichtsfigur von rotierenden Himmelskörpern auch unter dem Einfluß von Inhomogenitäten quantitativ untersuchen, werden bei Wikipedia angesprochen, allerdings auch hier ohne daß selbst in den einfachsten Fällen eine theoretische Herleitung der Abplattung beschrieben wird.

Folgende Annahmen sind für eine Herleitung denkbar und sollen hier im Hinblick auf die Verformung der Erdkugel durch die Fliehkraft und eine Berechnung der Radiendifferenz geprüft werden:

Die Fliehkraft verformt die Erde so, daß ihre Oberfläche eine Äquipotentialfläche wird.
Die Erde verformt sich so, daß ihre Oberfläche senkrecht zu der aus Gravitation und Fliehkraft resultierenden Gesamtkraft wird.

Erste Annahme: Die Erdoberfläche wird Äquipotentialfläche

Daß bei einer plastisch verformbaren Erde die Oberfläche die Form einer Äquipotentialfläche annimmt, bedeutet: Hätte sie relativ dazu nämlich Täler, dann würde Materie dorthin strömen und die Oberfläche erhöhen, bis diese Täler aufgefüllt sind.

Dies soll im Folgenden kurz skizziert werden. Die Gravitationskraft, also das Gewicht eines Element \(m,\) ist \[ G = -m g, \] Ihr Potential ist als Funktion der Höhe \(h\) über dem Boden \[ \varphi =mg \left(R_\text{E}+h\right). \] Darin ist \(R_\text{E}=6369.6\) km der Radius einer idealen Erdkugel ohne Verformung durch Fliehkraft.

Es ist \[ G \equiv -\frac{\partial\varphi}{\partial h}. \]

Die Flieh- oder Zentrifugalkraft \(F\) nimmt bei der geografischen Breite \(\beta\) mit dem Abstand \(\varrho(\beta)= R_\text{E}\cos\beta\) von der Rotationsachse zu \begin{align} F(\beta) &= m\varrho(\beta)\, \omega^2\\ &= m R_\text{E}\cos\beta\;\omega^2. \end{align} Hierin ist \(\omega = 7.292115\cdot10^{-5}/\text{s}\;\) bzw. \(\;\omega^2= 53.175\cdot10^{-10}/\text{s}^2\).

Durch die Zentrifugalkraft verformt sich die Erdkugel zu einem Rotationsellipsoid. Ihr Radius nimmt entlang eines Meridians die Breitenabhängigkeit \[ R(\beta) = \frac{3h}{2}\,\cos(2\beta)+R_\text{E} - \frac{h}{2} \] an, wobei das Erdvolumen erhalten bleibt. Die Zentrifugalkraft \(F\) ist viel schwächer als die Gravitationskraft. Sie hat ihr Maximum am Äquator mit 0.003386 m/s^2, also mit nur gut 0.3 Prozent der Gravitationskraft \(G\).

Zu ihr gehört das Potential \[ \psi(\beta) = -m\frac{\varrho(\beta)^2}{2}\,\omega^2. \] Damit ist \[ F(\beta) = -\frac{\partial \psi}{\partial \varrho}. \] An den Polen wirkt keine Fliehkraft. Dort bei \(\beta=90°\) besteht bei einer Absenkung des polaren Erdradius um \(2h\) (siehe Volumenerhaltung) das Gesamtpotential an der Meeresoberfläche nur aus dem Gravitationspotential \[ \Phi_\text{P} = mg\left(R_\text{E}-2h\right). \] Am Äquator bei \(\beta=0°\) senkt die Fliehkraft das Gesamtpotential an der Meeresoberfläche ab auf \begin{align} \Phi_\text{Ä} &= mg\left(R_\text{E} +h\right)\\ &- m\,\frac{(R_\text{E}+h)^2}{2}\,\omega^2. \end{align} Wenn auf einer Äquipotentialfläche das Potential am Äquator gleich dem an den Polen sein soll, also \(\Phi_\text{Ä} = \Phi_\text{P}\), dann muß gelten \begin{align} & \underbrace{g\left(R_\text{E}+h\right)-\frac{(R_\text{E}+h)^2}{2}\,\omega^2}_\text{Äquator}\\ &=\underbrace{g\left(R_\text{E} -2h\right)}_{\text{Pol}}. \end{align} Diese Potentialbilanz führt auf eine quadratische Gleichung \[ \boxed{ h^2 + p h + q=0} \] für die Höhe \(h\) mit \begin{align} p &= -2\left(\underbrace{\frac{3g}{\omega^2}}_{5.53\cdot10^9} -\underbrace{R_\text{E}}_{6.369.6\cdot10^6} \right)\\&\approx-\frac{6g}{\omega^2} =-1.1056\cdot10^7\text{ km,}\\ %& \approx 2\frac{3g}{\omega^2} \approx 1.12\cdot10^{10}\text{ km,}\\ q &=R^2_\text{E} = 4.0572\cdot10^7\text{ km}^2. \end{align}

Die quadratische Gleichung hat die beiden Lösungen \begin{align} h &=-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}\\ &=\frac{p}{2}\left(-1 \pm\sqrt{1-\frac{4q}{p^2} } \right)\\ &\approx\frac{p}{2}\left( -1\pm\left(1-\frac{2q}{p^2}\right)\right)\\ &=\left\{\begin{array}{l} \displaystyle-\frac{q}{p} =\frac{R^2_\text{E}}{\displaystyle\frac{6g}{\omega^2} - 2R_\text{E}}\\ \approx\displaystyle\frac{\omega^2R^2_\text{E}}{6g} =3.669\text{ km}\\ -p + \displaystyle\frac{q}{p} \end{array}\right. \end{align} Mit dem oberen Vorzeichen der Wurzel ergibt sich als Höhe \[ \boxed{ h=-\frac{q}{p}=3.669\text{ km},} \] ein etwa um den Faktor 2 zu niedriger Wert. Der Betrag der Höhe wäre immerhin etwa halb so groß wie die erwarteten 7 km.

In der obigen quadratischen Gleichung und damit auch in ihren Lösungen kommt die Dichte der Erde nicht vor. Die obige Näherung für ihren Koeffizienten \(p\) läßt aber erkennen, daß die äquatorielle Erhöung proportional zur Erdbeschleunigung \(g(R_\text{E})=GM_\text{E}/R_\text{E}^2\) ist mit der Gravitationskonstanten \(G.\) Deshalb würde die Erhöhung \(h\) am Äquator umso kleiner bleiben, je größer die Erdmasse \(M_\text{E}\) wäre.

Wenn – anders als bisher hier verwendet – die Erde nicht homogen ist sondern kugelsymmetrisch bei gleichem Volumen und gleicher Masse die Dichte in ihrem Kern wesentlich höher ist als in ihrer Kruste, dann blieben im Außenraum Gravitations- wie Zentrifugalpotential sowie die Erdbeschleunigung \(g\) ungeändert. Solche Inhomogenität hätte, deshalb keinen Einfluß auf die Berechnung der Abplattung.

Mit dem unteren Vorzeichen in der obigen Lösung der quadratischen Gleichung wäre die Höhe \(h\) riesig und deshalb ungeeignet.

Läßt sich die Differenz zum Meßwert erklären? Ein Versuch:

Würde man bei der Erdrotation die Winkelgeschwindigkeit \(\omega\) höher als \(7.29\cdot10^{-5}\)/s mit \(\omega=10.05\cdot10^{-5}\)/s, also etwa 38 Prozent höher, annehmen, dann ergäbe sich – zumindest betragsmäßig – wie erwartet die Höhe \(h=7\,\text{km}\). Solch höhere Rotationsrate könnte in der Frühzeit der Erde vorgelegen haben. Beobachtet wird, daß sich die Tagesdauer pro hundert Jahre um etwa 1.7 ms auf den heutigen Wert verlängert. Die gemessene Radiendifferenz könnte sich also vor langer Zeit eingestellt und sich danach erhalten haben.

Tatsächlich trägt wegen Erhaltung des Drehimpulses \(\vec{L}=J\vec{\omega}\) schon die Erdabplattung selber zur Verlangsamung der Rotation bei, weil die Verschiebung von Masse in Richtung zum Äquator und damit zu größerem Rotationsradius das Trägheitsmoment \(J\) der Erde vergrößert.

Fragen dazu:

Wie groß ist das Tragheitsmoment der jetzigen Erde (Quelle)? \begin{align} I&= \frac{m}{5}\cdot(a^2+b^2)\\ &= 5.9722\cdot10^{24}\cdot0.4\cdot 6.378^2\cdot10^6\text{ kg m\(^2\)}\\ &=9.762930\cdot10^{31}\text{ kg m\(^2\)}.\\ \end{align}
Wie stark ändert sich durch die Abplattung das Trägheitsmoment der Erde?
Bei einer Erhöhung des Radius einer homogenen Erdkugel am Äquator um 7 km vergrößert sich das Trägheitsmoment auf \begin{align} I&= \frac{m}{5}\cdot(a^2+b^2)\\ &= 5.9722\cdot10^{24}\cdot0.4\cdot 6.385^2\cdot10^6\text{ kg m\(^2\)}\\ &=9.78463\cdot10^{31}\text{ kg m\(^2\)}, \end{align} also um ≈ 0.22 Prozent. Tatsächlich ist die Dichte der Erde außen geringer als im schwereren Kern. Das schwächte diese Vergrößerung des Trägheitsmoments ab.
Wegen der Erhaltung des Drehimpulses würde sich die Winkelgeschwindigkeit der Erdrotation dabei um etwa 0.22 Prozent; erniedrigen, was wegen der damit abnehmenden Fliehkraft einer Abplattung entgegenwirken würde.

Volumenerhaltung

Wenn die Fliehkraft durch eine Massenverschiebung in äquatorialer Richtung die Erdoberfläche zu einer Äquipotentialfläche macht und dabei das Volumen konstantbleiben soll, das muß bei einer Vergrößerung des äquatorialen Radius eines Rotationsellipsoids von \(a\) auf \(a+h\) der polare Radius von \(c\) auf \(c-2h\) abnehmen. Die Radiendifferenz wird dadurch \(\Delta R = 3h\).

Zweite Annahme: Die Erdoberfläche stellt sich so ein, daß sie senkrecht zur resultierenden Gesamtkraft aus Schwerkraft \(g\) und Fliehkraft \(f\) liegt.

Solange sie davon abweicht, wirkt parallel zu ihr eine Kraftkomponente, die Materie bei einer plastisch verformbaren Erde ausgleichend verschiebt.

Abb. 2: In der gezeichneten Meridianebene liegt die Erdachse waagerecht. Die Fliehkraft \(f\) (blau) wirkt senkrecht dazu. Sie nimmt vom Äquator zu den Polen hin auf Null ab und ist hier gegenüber der zum Erdmittelpunkt weisenden Gravitationskraft \(g\) (rot) stark übertrieben gezeichnet. Der Winkel \(\alpha\) sei hier und im Folgenden im Uhrzeigersinn zu zählen.

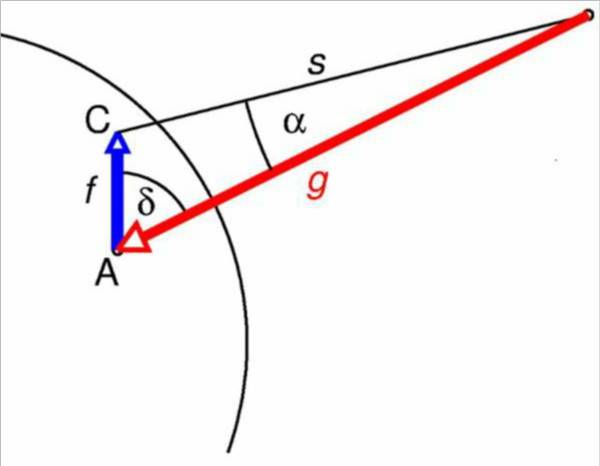
Es sei \(\beta\) die geografische Breite und die \(y\)-Achse die Erdachse. Der Summenvektor \begin{align} \vec{s} &=\vec{g}+\vec{f}\\ &=g_0\begin{pmatrix}\cos\beta\\\sin\beta\end{pmatrix} +f_0\begin{pmatrix}\cos\beta\\0\end{pmatrix}\\&= g_0\begin{pmatrix} \cos\beta(1 + k)\\\sin\beta \end{pmatrix} \end{align} von Schwerkraft \(\vec{g}\) und der selbst am Äquator viel schwächeren Fliehkraft \(\vec{f}\) bildet mit dem zum Erdmittelpunkt M ausgerichteten Vektor \(\vec{g}\) mit \begin{align} k&:=\frac{f_0}{g_0} \approx 0.003\\ \vec{s}\cdot\vec{g} & = g_0^2 (1+k\cos^2\beta)\\ |\vec{s}| &=g_0%\sqrt{1+2k\cos\beta+k^2}\\ \sqrt{1+k\left(2+k\right)\cos^2\beta}\\ |\vec{g}| &=g_0 \end{align} den Kraftrichtungswinkel \(\alpha\) mit \begin{align} \cos\alpha &=\frac{\vec{s}\cdot\vec{g}}{|\vec{s}||\vec{g}|}\\ &=\frac{1+k\cos^2\beta}{\sqrt{1+k\left(2+k\right)\cos^2\beta}}. \end{align} oder \begin{align} \alpha(\beta) &= \arccos\left(\frac{1+k\cos^2\beta} {\sqrt{1+k\left(2+k\right)\cos^2\beta}}\right). \end{align}

Abb. 3: Am Äquator \((\beta=0°)\) und an den Polen (Nordpol bei \(\beta=90°\), Südpol bei \(\beta=-90°)\) wirkt die Summenkraft \(\vec{g}+\vec{f}\) mit \(\alpha=0^\circ\) genau in Richtung auf den Erdmittelpunkt. Am weitesten weicht \(\alpha\) bei mittleren Breiten davon ab. Wie Zeichnung zeigt, läßt sich die Breitenabhängigkeit des Winkels \(\alpha\) sehr gut durch eine Sinusfunktion, wie sie unten berechnet wird, annähern.

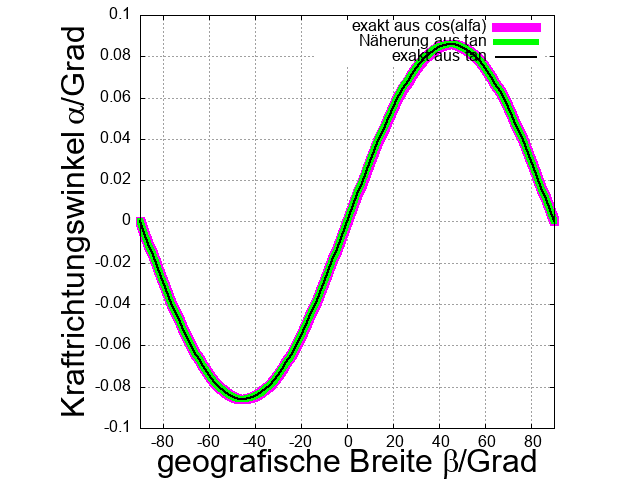
Der Winkel \(\alpha\) zählt gegen die Erdradialrichtung. Um den gleichen Winkel müßte die Erdoberfläche von der Horizontalen abweichen, wenn sie im rechten Winkel zur Summe aus Gravitations- und Fliehkraft liegen soll. Für ihre Steigung entlang eines Meridians müßte also gelten \[ R'(\beta)\equiv\frac{\partial R}{R_\text{E}\partial\beta} = -\tan\alpha. \] Mit \begin{align} &\tan\alpha =\frac{\sin\alpha}{\cos\alpha} =\frac{\sqrt{1-\cos^2\alpha}}{\cos\alpha}\\ &=-\frac{x-90°}{|x-90°|}\sqrt{\frac{1}{\cos^2\alpha}-1}. \end{align} erhält man nach kurzer Rechnung \begin{align} &\tan\alpha(\beta)\\ &=\frac{x-90°}{|x-90°|}\sqrt{\frac{1+k\left(2+k\right)\cos^2\beta}{\left(1+k\cos^2\beta\right)^2} - 1}\\ &= \frac{x-90°}{|x-90°|}\frac{k\cos\beta\sqrt{1-\cos^2\beta}}{1+k\cos^2\beta}\\ &=\frac{x-90°}{|x-90°|}\frac{k\cos\beta\sin\beta}{1+k\cos^2\beta}\\ &=\frac{k}{2(1+k\cos^2\beta)}\,\sin(2\beta)\\ &\approx \frac{k}{2}\sin(2\beta). \end{align} Die Näherung für \(k\ll1\) ist in Abb. 3 mit den urprünglichen Funktionen zu vergleichen. Damit wäre der Erdradius als Funktion der geografischen Breite \begin{align} R(\beta)&\approx R_\text{E} \frac{k}{2} \int \sin(2\beta')\text{ d}\beta'+R(0)\\ &= -R_\text{E}\frac{k}{4}\,\cos(2\beta)+R(0). \end{align}

Abb. 4: Der Erdradius, hier gezeichnet relativ zum mittleren Erdradius, ist wegen der Fliehkraft am Äquator, also bei der geografischen Breite \(\beta=0\), größer als an den Polen bei \(\beta=\pm90°\).

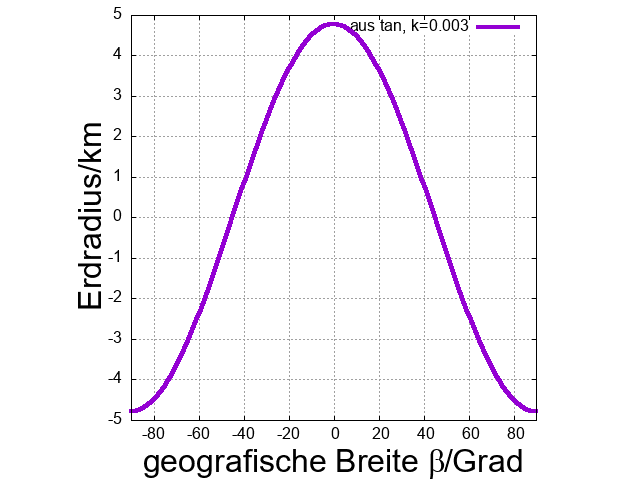
Die gesuchte Radiendifferenz ergäbe sich schließlich als \[ \boxed{ \begin{align} \Delta R&= R(0)-R(\pm90°) \approx \frac{k}{2} R_\text{E}\\&=0.5\cdot0.003\cdot 6369.3 \text{ km}\\ &= 9.554 \text{ km,} \end{align} } \] wie auch Abb. 4 zeigt. Dieser hier berechnete Wert ist also um 11.8 km zu klein und damit weniger als halb so groß wie der gemessene Wert von 21.38 km.

Dies müßte noch geklärt werden, wie es bei der ersten Annahme oben auch schon versucht worden ist.

Ergebnis und Diskussion:

Aus Gewichts- und Fliehkraft sollte die Abplattung der Erdkugel hergeleitet werden. Dazu war eine zusätzliche Annahme erforderlich. Verwendet habe ich dazu (1) das Potential der Gesamtkraft oder (2) ihre Richtung.

In beiden Fällen habe ich bemerkenswerterweise fast gleiche aber mit 3 km bis 4 km statt der erwarteten 7 km (entsprechend 21 km Radiendifferenz) zu geringe äquatoriale Erhöhungen erhalten, wofür – wie hier beschrieben – eine Erklärung über die geophysikalische Geschichte der Erde denkbar ist.

In dem eingangs genannten Artikel von Fitzpatrick, wo wie hier in der ersten Annahme postuliert wird, daß die Erdoberfläche sich als Äquipotentialfläche einstellt, ergibt sich im Gegensatz zu meiner Rechnung eine mit 27.3 km gegenüber 21.38 km um etwa 6 km etwas zu große Radiendifferenz. Fitzpatrick deutet als Begründung an, daß er die Erde als homogen angenommen hat, obwohl ihre Dichte im Inneren viel dichter als in der Erdkruste ist. Er quantifiziert das aber nicht.

Es bleibt also zu klären, warum seine und meine hier berechnete Radiendifferenz voneinander und vom Meßwert abweichen, obwohl beide Rechnungen von der ortsabhängigen Gravitations- und Fliehkraft und deren Potentialen ausgehen und beide eine Äquipotenfläche als Erdoberfläche fordern.

Fitzpatrick verwendet als Fliehkraftpotential \(\chi\), wie es in der dortigen Gleichung (913) berechnet und in (914) bis (917) verwendet wird. Laut (913) wäre es mit den hier verwendeten Variablen und \(\theta=90°-\beta\) \begin{align} \chi(r,\beta)&=-\frac{\omega^2 R^2_\text{E}}{3}\left(1-P_2(\sin\beta) \right)\\ &= -\frac{\omega^2 R^2_\text{E}}{3}\left(1-\frac{3\sin^2\beta-1}{2} \right)\\ &=-\frac{\omega^2 R^2_\text{E}}{2} \cos^2\beta \end{align} in Übereinstimmung mit dem hier benutzten \[ \psi(\beta) = -m\,\frac{\varrho^2(\beta)}{2}\,\omega^2. \] Das Gravitationspotential \(\varphi\) wird bei Fitzpatrick nicht explizit angegeben. Aus (916) wäre aber mit der Gravitationskonstanten \(G= 6.672 59\cdot10^{-11} \text{N m}^2 / \text{kg}^2,\) dem mittleren Radius \(R=6.371\cdot10^6\) m und der Erdmasse \(M = 5.972\cdot10^{24}\text{ kg}\) zu schließen \[ \varphi(\beta) = \frac{GM}{R}\left(1+\frac{2}{15}\,\varepsilon\left(3x^2-1\right) \right). \]

Aus \(\varphi+\chi=\text{const}\) folgert der Author schließlich mit \(\omega = 7.29245\cdot10^{-5}\)/s \begin{align} \varepsilon&=\frac{R_\text{Äqu}-R_\text{Pol}}{R} = \frac{5}{4}\,\frac{\omega^2 R^3}{G M}\\ &=1.25\frac{7.29245^2\cdot10^{-10}\cdot6.371^3\cdot10^{18}} {6.672 59\cdot10^{-11}\cdot 5.972\cdot10^{24}} %\\&=1.25\frac{53.18\cdot10^{-10}\cdot6.371^3\cdot10^{18}} %{6.672 59\cdot10^{-11}\cdot 5.972\cdot10^{24}} \\ &=4.31\cdot10^{-3} \end{align} und damit \[ \Delta R = R\; \varepsilon=27.3\text{ km}. \]