Gravitationspotential einer Kugel
Dieses Thema ist noch in Arbeit.
Es soll das Potential einer homogenen Kugel des Radius \(R\)
und der Masse \(M\) berechnet werden.
Vorübungen
1) Die Fläche eines Kreises mit dem Radius \(R_f\) läßt sich
mit dem infinitesimalen
Flächenelement \(\text{ d}F = r \text{ d}\varphi\text{ d}r\)
berechnen als
\[
F_\text{Kreis} =
\underbrace{\int\limits_0^{R_f}
\underbrace{\int\limits_{-\pi}^\pi r \text{ d}\varphi}_{2\pi R_f r} \text{ d}r}
_{2\pi R_f^2/2}
= \pi R_f^2.
\]
2) Volumen einer Kugel mit dem Radius \(R\):
Hier ist als infinitesimales Volumenelement \(\text{ d}V
= r^2 \sin\vartheta\text{ d}\vartheta\text{ d}\varphi\text{ d}r\)
zu verwenden, womit folgt
\begin{align}
V_\text{Kugel} &=
\underbrace{\int\limits\limits_0^R
\underbrace{\int\limits_{-\pi}^\pi
\underbrace{\int\limits_0^\pi r^2\sin\vartheta\text{ d}\vartheta}_{-r^2[\cos\vartheta]_0^\pi=2r^2}
\text{ d} \varphi}_{4\pi r^2} \text{ d}r}
_{\frac{R^3}{3}\,4\pi}\\
&= {\frac{4\pi}{3}R^3}.
\end{align}
3) Das Potential einer Kreisfläche des Radius \(R_f\)
mit homogener Massenflächendichte
\[
\mu_f = \frac{M}{\pi R^2_f}
\]
als Schnitt einer Kugel bei \(\vartheta=\vartheta_0\) ist
am Meßort
\(\vec{z}=\begin{pmatrix}0\\0\\z\end{pmatrix}\) gleich
\[
\Phi_\text{Kreis}(z) = \int\limits_0^{R_f} \int\limits_{-\pi}^\pi
\frac{G\mu_f}{\varrho(z)}\, r \cos\varphi\text{ d}\varphi \text{ d}r.
\]
Mit dem Abstand
\begin{align}
\varrho(z)&={\sqrt{(z-R_f\sin\vartheta_0)^2+(R_f\cos\vartheta_0)^2}}\\
&=\sqrt{z^2-2zR_f\sin\vartheta_0+R_f^2}
\end{align}
wird es
\begin{align}
\Phi_\text{Kreis}(z)\\ &=
\int\limits_0^{R_f} \int\limits_{-\pi}^\pi
\frac{G\mu_f}{\sqrt{z^2-2zR_f\sin\vartheta_0+R_f^2}}\, r \cos\varphi\text{ d}\varphi\text{ d}r\\
&=\frac{GM }{\sqrt{z^2-2zR_f\sin\vartheta_0+R_{f}^2} }.
\end{align}
Spezielle Fälle:
- Bei \(\vartheta_0=\pm\pi\) ziehen sich der Kreis
und damit die Masse auf einen Punkt zusammen,
und das Potential wird
\[
\Phi_\text{Kreis}(z)= \frac{GM}{z\mp R_f}
\]
- Bei \(\vartheta_0=0\) wird
\[
\Phi_\text{Kreis}(z) = \frac{GM}{\sqrt{z^2+R_f^2}}.
\]
Man könnte erwarten, daß dieses Potential einer Punktmasse im Mittelpunkt des Kreises
entspräche.
Wie die Formel aber zeigt, müßte die Punktmasse
nicht dort sondern auf der \(z\)-Achse
im gleichen Abstand zum Meßort liegen wie die Punkte auf dem Kreisrand.
Das Potential außerhalb einer Kugel mit homogener Massendichte
\[
\mu_v=\frac{M}{\displaystyle\frac{4\pi}{3}R^3}
\]
ergibt sich folgendermaßen:
Ein Meßort \(\vec{z}=\begin{pmatrix}0\\0\\z\end{pmatrix}\) hat von einem Punkt
\(\vec{x_k} =
R\begin{pmatrix}\sin\vartheta\cos\varphi\\\sin\vartheta\sin\varphi\\\cos\vartheta \end{pmatrix}
\)
in der Kugel den Abstand
\begin{align}
\varrho(z)&=|\vec{z}-\vec{x_K}|\\
&={\sqrt{(z-R\cos\vartheta)^2+(R\sin\vartheta)^2}}\\
&=\sqrt{z^2-2zR\cos\vartheta+R^2}.
\end{align}
Damit wird das Potential
\begin{align}
&\Phi_\text{Kugel}(z) \\
&= \int\limits_0^R \int\limits_0^\pi \int\limits_0^{2\pi}
\frac{G\mu_v}{\sqrt{z^2-2zR\cos\vartheta+R^2}}\, r^2\sin\vartheta
\text{ d}\varphi\text{ d}\vartheta \text{ d}r\\
&= 2\pi\int\limits_0^\pi
\int\limits_0^R \frac{G\mu_v}{\sqrt{z^2-2zR\cos\vartheta+R^2}}\,r^2\sin\vartheta
\text{ d}r \text{ d}\vartheta\\
&=2\pi \int\limits_0^\pi\frac{G\mu_v}{\sqrt{z^2-2zR\cos\vartheta+R^2}}
\frac{R^3}{3}\,\sin\vartheta\text{ d} \vartheta\\
&=%\frac{2\pi R^3G\mu_v}{3}\int\limits_0^\pi
\frac{GM}{2}
\int\limits_0^\pi\frac{\sin\vartheta}{\sqrt{z^2+R^2-2zR\cos\vartheta}}
\text{ d}\vartheta
\end{align}
mit der dimensionslosen Abkürzung \(A:=\displaystyle\frac{z^2+R^2}{2zR}\) wird
das Potential zu
\begin{align}
\Phi_\text{Kugel}(z) &= \frac{GM}{2\sqrt{2zR}}
\int\limits_0^\pi\frac{\sin\vartheta}{A-\cos\vartheta} \text{ d}\vartheta\\
&=\frac{GM}{\sqrt{2zR}}\left(\sqrt{A+1} -\sqrt{A-1} \right)\\
%&=GM\frac{4R}{\sqrt{2zR}}=GM\sqrt{\frac{8R}{z}}.
&=\frac{GM}{\sqrt{2zR}}\,\frac{2R}{\sqrt{2zR}}
=\frac{GM}{2zR}\cdot2R=\frac{GM}{z}.
\end{align}
Das Potential der homogenen Kugel mit beliebigem Radius
ist außerhalb der Kugel also genau so groß,
als wenn ihre Masse in ihrem Mittelpunkt konzentriert wäre,
denn das
Potential
einer Punktmasse \(M\) im Ursprung bei \((0,0,0)\),
ist am Ort \((0,0,z)\) auf
der \(z\)-Achse,
also im Abstand \(r=z\) von der Masse,
gleich
\[
\varphi_0(r)=\frac{GM}{r}.
\]
(Gravitationskonstante
\(
G = 6.67259 \cdot 10^{-11}\text{ N · m}^2/\text{kg}^2).
\)
In einer Kugel des Volumens \(V_1\) und der Dichte \(\mu_1\)
befinde sich konzentrisch eine Kugel mit dem kleineren
Volumen \(V_2\) und der höheren Dichte \(\mu_2\).
Ihr gemeinsames Potential läßt sich linear zusammensetzen als
\begin{align}
\Phi(z) &= \frac{G}{z}\left( V_1\mu_1-V_2\mu_1+V_2\mu_2\right)\\
&= \frac{GM}{z}.
\end{align}
Solches liegt bei der Erdkugel vor.
Ein schwerer Erdkern ist umgeben von einem
Erdmantel und einer Erdkruste, beide mit geringerer Dichte als der Kern.
Das Potential im Außenraum dieser radial inhomogenen Kugel
bleibt also gleich dem einer homogenen Kugel
der gleichen Gesamtmasse.
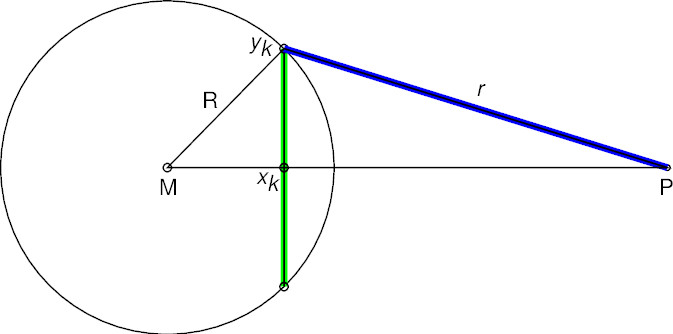
Masse auf Kreisrand:
Ist die Masse auf dem Rand eines Kreises in der
\(x,z\)-Ebene,
der also senkrecht zur \(x\)-Achse liegt, mit gleichmäßiger
Liniendichte \(M/(2\pi R)\) verteilt,
dann ist der Abstand vom Punkt \(M=(0,0,0)\)
zu einem Punkt \(P=(x,0,0)\) einheitlich
mit \(y^2_k=R^2-x_k^2\) gleich
\begin{align}
r(x_k) &= \sqrt{(x-x_k)^2 + y_k^2} \\
&=\sqrt{x^2-2xx_k + R^2}.
\end{align}
Im Spezialfall \(x_k=\pm R\) ist
die Gesamtmasse \(M\) an einem oder dem gegenüberliegenden Punkt konzentriert.
Sie haben zu \(P\) den Abstand \(r=x\mp R.\)
Der Abstand \(r\) zum Punkt \(P\) ist auf dem ganzen Kreis gleich.
Die Punkte auf einem vollen Kreisbogen
erzeugen wegen der einheitlichen Liniendichte der Masse
zusammen das Potential
\begin{align}
&\varphi_\text{Bogen}(x,x_k)\\ &= \frac{GM}{\sqrt{x^2-2xx_k + R^2}}.
\end{align}
Dieses Potential ist etwas kleiner als dasjenige, was entstünde,
wenn die Masse \(M\)
im Kreismittelpunkt, also bei \(x=x_k\) konzentriert läge, nämlich
\begin{align}
&\varphi_\text{Kreismitte}(x,x_k)\\ &= \frac{GM}{\sqrt{x^2-2xx_k + x_k^2}}.
\end{align}
Masse auf Kreisfläche:
Die von einem Kreisrand umfaßte Fläche läßt sich zusammensetzen
aus den darin konzentrisch liegenden Kreisbögen.
Deren Potentiale addieren sich.
Das Potential einer ganzen Kreisfläche,
auf die sich die Masse \(M\) mit der einheitlichen
Flächendichte
\[
\frac{M}{\pi y_k^2}= \frac{M}{\pi \left(R^2-x_k^2 \right)}
\]
verteilt,
ergibt sich aus den Beiträgen dieser Kreise zu
\begin{align}
&\varphi_\text{Fläche}(x_k) = \int\limits^R_{-R}
\varphi_\text{Bogen}(r,x_k) \text{ d}x_k\\
&= -2\pi GM \left[\frac{\sqrt{R^2+x^2-2x x_k}}{x}\right]_{-R}^R \\
&= \frac{-2\pi GM}{x}\left(|R-x| - |R+x| \right)\\
&= \frac{4\pi R GM}{x} \text{bei }x>R.
\end{align}
Masse auf Kugelvolumen homogen verteilt:
Die gemeinsame Wirkung aller solcher Kreisflächen müßte
bei einer Dichte
\(\displaystyle\frac{M}{(4/3)\pi R^3}\) das Potential einer im Mittelpunkt
der Erde konzentrierten Masse ergeben.
\begin{align}
\varphi_\text{Kugel} &= \int\limits_{-R}^{R} \varphi_\text{Fläche}(x_k) \text{ d}x_k\\
&=\int\limits_{-R}^R \frac{4RGM}{x}\,\frac{\text{d}x_k}{R^2-x_k^2}\\
&=\frac{2GM}{x}
\tanh^{-1}\left(\frac{x}{R}\right).
\end{align}
© Günter Green
zu den Physikthemen
21-Feb-2023